Rumus Lilliefors
Artikel kali ini merupakan lanjutan dari artikel sebelumnya yang berjudul “Uji Normalitas“. Dalam bahasan ini, kita membahas tentang rumus lilliefors. Metode Lilliefors menggunakan data dasar yang belum diolah dalam tabel distribusi frekuensi. Data ditransformasikan dalam nilai Z untuk dapat dihitung luasan kurva normal sebagai probabilitas komulatif normal. Probabilitas tersebut dicari bedanya dengan probabilitas kumulatif empiris. Beda terbesar dibanding dengan tabel Lilliefors.
Keterangan :
Xi = Angka pada data
Z = Transformasi dari angka ke notasi pada distribusi normal
F(x) = Probabilitas komulatif normal
S(x) = Probabilitas komulatif empiris
Syarat Uji Lilliefors
a. Data berskala interval atau ratio (kuantitatif)
b. Data tunggal / belum dikelompokkan pada tabel distribusi frekuensi
c. Dapat untuk n besar maupun n kecil.
Signifikansi Uji Lilliefors
Signifikansi uji, nilai | F (x) – S (x) | terbesar dibandingkan dengan nilai tabel Lilliefors.
Jika nilai | F (x) – S (x) | terbesar < nilai tabel Lilliefors, maka Ho diterima ; Ha ditolak. Jika nilai | F(x) – S(x) | terbesar > dari nilai tabel Lilliefors, maka Ho ditolak ; Ha diterima.
Contoh Uji Lilliefors
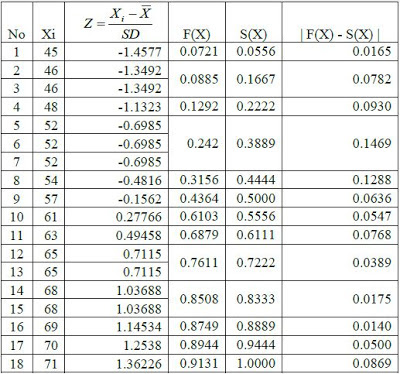
Berdasarkan data ujian statistik dari 18 mahasiswa didapatkan data sebagai berikut ; 46, 57, 52, 63, 70, 48, 52, 52, 54, 46, 65, 45, 68, 71, 69, 61, 65, 68. Selidikilah dengan α = 5%, apakah data tersebut di atas diambil dari populasi yang berdistribusi normal ?
Penyelesaian Rumus Lilliefors
Hipotesis Lilliefors:
- Ho : Populasi nilai ujian statistik berdistribusi normal
- H1 : Populasi nilai ujian statistik tidak berdistribusi normal
Nilai Kritis Lillifors:
Nilai α = level signifikansi = 5% = 0,05
Statistik Pengujian:
Nilai | F(x) – S(x) | tertinggi sebagai angka penguji normalitas, yaitu 0,1469.
Derajat Bebas
Df tidak diperlukan
Nilai Tabel Lilliefors atau Tabel Lilliefors
Nilai Kuantil Penguji Lilliefors, α = 0,05 ; N = 18 yaitu 0,2000. Tabel Lilliefors pada lampiran.
Daerah penolakan lilliefors
Menggunakan rumus | 0,1469 | < | 0,2000| ; berarti Ho diterima, Ha ditolak
Kesimpulan: Populasi nilai ujian statistik berdistribusi normal.
Penerapan Rumus Lilliefors di atas dalam MS Excel 2007 atau diatasnya, dapat anda pelajari pada artikel kami yang berjudul: “Lilliefors Excel“.
Untuk Metode chi-square telah dibahas dalam artikel sebelumnya: “Uji Normalitas“.
Untuk Metode yang lain, Kolmogorov Smirnov dan Saphiro Wilk akan dibahas dalam artikel lainnya. Demikian di atas telah kami jelaskan untuk para peneliti tentang rumus lilliefors dengan cara yang singkat dan padat. Semoga dapat dipahami dan bermanfaat untuk penelitian anda.
Untuk Pengujian Normalitas dalam SPSS, Baca: Normalitas Pada SPSS.
By Anwar Hidayat
Sebaiknya gunakan uji shapiro wilk dengan SPSS atau hitung manual seperti dalam artikel saya
bagaimana untuk mencari uji normalitasnya jika sampel berjumlah 23..??
tolong bantuannya min…
Lihat artikel saya tentang tabel lilliefors
Bisa
tabel liliefors yg mana yaaa ?? bingung saya min….
saya punya sampel 12 dan 48 jumlahnya…..
mohon pencerahanya ya min.
trim..
kalau sampel dengan jumlah 19 apakah bisa menggunakan uji shapiro wilk? tolong bantuannya 🙂
F(x) adalah nilai probabilitas pada kurve normal (gunakan tabel Z lengkung kurve normal) dari nilai Notasi yang sudah distandarisasi (gunakan tabel Z). Jika kesulitan baca artikel saya tentang Lilliefors Excel, di dalamnya diajari cara menghitung Zi dan F(x). S(x) adalah probabilitas empiris, yaitu nilai urutan ke-i dibagi total (count) banyaknya i.
nilai tabel untuk F(X) dan S(X) it di dpat dari mana ka ???
Coba anda urutkan sampel yang diuji secara ascending, artinya dari yang terkecil hingga yang terbesar. Harusnya tidak ada nilai negatif.
Hasil F(X) – S(X) ada nilai negatif nya, masksud dari nilai negatif tersebut apa ya min ? Padahal angka tersebut yang terbesar dari yang lainnya.
Tlg bntuanya min,,
Coba anda baca artikel Lilliefors Excel
Sdh saya lakukan.
Mksd saya seperti contoh di atas, 0,1469 trsbut di dapat dari 0,242 – 0,388. Hsil nya bukankah -0,1469 ?
Nah nilai nim nya itu mksd nya ap ? Knp bsa bernilai plus ?
Mohon bntuan nya min. Saya punya kndala dsna.
Ya
min, apakah data angketnya harus di urutkan dulu dari yang terkecil
Min, saya diminta mencari alasan pemilihan uji normalitas antara K-S, S-W, atau lilliefors. Karena rujukan penelitian sejenis saya ada yang pakek K-S, S-W, ada juga yang pakai lilliefors tapi tidak disertai alasan pemilihan metode uji tersebut. Data saya terdiri dari 34 nilai untuk kelas kontrol dan 34 nilai untuk kelas eksperimen yang tidak disusun dalam tabel distribusi. Sekiranya saya bisa baca di artikel mimin yg mana? Terimakasih banyak. Semoga berkah.
Baca artikel saya yang berjudul: pilihan uji normalitas berdasarkan software-jumlah sampel
Waw terasa berkunang-kunang kalo sudah berhadapan dengan rumus…