Bootstrapping PLS SEM Metode Basic SMARTPLS
Pada artikel sebelumnya yang merupakan dasar dari artikel ini, yaitu pada artikel Inner Model PLS SEM dalam SMARTPLS, telah dibahas tutorial dan interpretasi dari inner model. Pada kesempatan ini akan dibahas lebih jauh yaitu tentang Bootstrapping PLS SEM. Bootstrapping adalah proses untuk menilai tingkat signifikansi atau probabilitas dari direct effects, indirect effects dan total effects. Selain itu, bootstrapping juga dapat menilai tingkat signifikansi dari nilai-nilai lainnya antara lain: r square dan adjusted r square, f square, outer loading dan outer weight.
Naman khusus untuk menilai signifikansi atau probabilitas dari r square dan adjusted r square serta f square, maka haruslah menggunakan metode yang sedikit berbeda dibandingkan dalam tutorial ini, yaitu menggunakan metode bootstrapping complete.
Pada bootstrapping PLS SEM metode complete, semua nilai yang dapat dianalisis dalam analisis partial least square, dilakukan bootstrapping agar menghasilkan nilai probabilitasnya. Misalnya nilai R Square dan Adjusted R Square. Untuk metode complete akan dibahas pada artikel berikutnya, yaitu pada artikel yang berjudul Bootstrapping Complete PLS SEM dan Blindfolding.
Pada kesempatan ini hanya akan dibahas bootstrapping PLS SEM metode basic, yaitu hanya menghasilkan tingkat signifikansi antara lain: outer loading, outer weight, direct effects, indirect effects dan total effects.
Sedangkan analisis blindfolding dalam PLS SEM digunakan untuk menilai relevansi dari prediksi terhadap variabel endogen. Bahasan tentang ini akan dikupas nantinya dalam artikel berikutnya bersamaan dengan artikel Bootstrapping Complete PLS SEM dan Blindfolding.
Bootstrapping PLS SEM Metode Basic
Langkahnya adalah pada menu SMARTPLS anda, klik run analysis, kemudian pilih jenis analisis bootstrapping. Akan muncul jendela atau window sebagai berikut:

Sesuai dengan gambar jendela analisis bootstrapping PLS SEM diatas, maka anda isikan nilai subsamples sebesar 500 atau lebih. Nilai makin tinggi maka makin baik. Namun disesuaikan dengan performance atau kekuatan dari komputer anda. Sebab nilai ini menunjukkan banyaknya resampling atau pengulangan yang dilakukan oleh komputer untuk mendapatkan nilai probabilitas atau nilai signifikansi.
Untuk pilihan lain-lain biarkan secara default sesuai gambar diatas, termasuk pada tab partial least square dan weighting. Sedangkan isian significance level, anda isi dengan batas kritis atau tingkat kesalahan yang anda inginkan, yang mana pada umumnya adalah 0,05. Selanjutnya anda klik tombol CALCULATE. Dimana tampilannya sebagai berikut:

Kemudian selanjutnya anda bisa lihat output pada jendela output SMARTPLS. Hasilnya sebagai berikut:

Output itu adalah hasil dari analisis bootstrapping PLS SEM yang telah anda lakukan. Interpretasinya akan dibahas lebih lanjut di bawah ini.
Jika anda ingin melihat hasil output analisis yang kami lakukan dalam tutorial ini, bisa anda download hasil expor ke excel via link berikut: Output Bootstrapping PLS SEM.
Bootstrapping PLS SEM Direct Effects
Hasil dari analisis bootstrapping PLS SEM direct effects adalah sebagai berikut seperti dalam gambar di bawah ini:
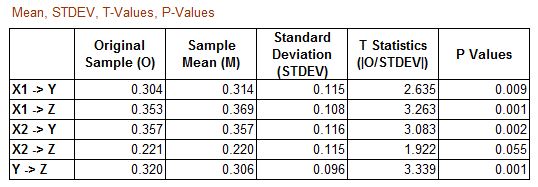
Sedikit review kembali, bahwa nilai path coefficients antar konstruk disini adalah nilai koefisien untuk melihat signifikansi dan kekuatan hubungan antar konstruk. Nilai tersebut digunakan untuk menguji hipotesis.
Nilai path coefficients berkisar antara -1 hingga +1. Semakin mendekati nilai +1, hubungan kedua konstruk semakin kuat. Hubungan yang makin mendekati -1 mengindikasikan bahwa hubungan tersebut bersifat negatif (Sarstedt dkk., 2017).
Berdasarkan tabel dalam gambar bootstrapping direct effects diatas, dapat diartikan sebagai berikut:
Direct Effects atau Pengaruh Langsung X1 Terhadap Y
Besarnya koefisien parameter untuk variabel X1 terhadap Y sebesar 0,304 yang berarti terdapat pengaruh positif X1 terhadap Y. Atau dapat diinterpretasikan bahwa semakin tinggi nilai X1 maka Y akan semakin meningkat pula. Peningkatan satu satuan X1 akan meningkatkan Y sebesar 30,4%. Berdasarkan perhitungan dengan menggunakan bootstrap atau resampling, dimana hasil uji koefisien estimasi X1 terhadap Y hasil bootstrap adalah sebesar 0,314 dengan nilai t hitung 2,635 dan standar deviasi 0,115. Maka nilai p value adalah 0,009<0,05 sehingga terima H1 atau yang berarti pengaruh langsung X1 terhadap Y bermakna atau signifikan secara statistik.
Direct Effects atau Pengaruh Langsung X1 Terhadap Z
Besarnya koefisien parameter untuk variabel X1 terhadap Z sebesar 0,353 yang berarti terdapat pengaruh positif X1 terhadap Z. Atau dapat diinterpretasikan bahwa semakin tinggi nilai X1 maka Z akan semakin meningkat pula. Peningkatan satu satuan X1 akan meningkatkan Z sebesar 35,3%. Berdasarkan perhitungan dengan menggunakan bootstrap atau resampling, dimana hasil uji koefisien estimasi X1 terhadap Z hasil bootstrap adalah sebesar 0,369 dengan nilai t hitung 3,263 dan standar deviasi 0,108. Maka nilai p value adalah 0,001<0,05 sehingga terima H1 atau yang berarti pengaruh langsung X1 terhadap Z bermakna atau signifikan secara statistik.
Direct Effects atau Pengaruh Langsung X2 Terhadap Y
Besarnya koefisien parameter untuk variabel X2 terhadap Y sebesar 0,357 yang berarti terdapat pengaruh positif X2 terhadap Y. Atau dapat diinterpretasikan bahwa semakin tinggi nilai X2 maka Y akan semakin meningkat pula. Peningkatan satu satuan X2 akan meningkatkan Y sebesar 35,7%. Berdasarkan perhitungan dengan menggunakan bootstrap atau resampling, dimana hasil uji koefisien estimasi X2 terhadap Y hasil bootstrap adalah sebesar 0,357 dengan nilai t hitung 3,083 dan standar deviasi 0,116. Maka nilai p value adalah 0,002<0,05 sehingga terima H1 atau yang berarti pengaruh langsung X2 terhadap Y bermakna atau signifikan secara statistik.
Direct Effects atau Pengaruh Langsung X2 Terhadap Z
Besarnya koefisien parameter untuk variabel X2 terhadap Z sebesar 0,221 yang berarti terdapat pengaruh positif X2 terhadap Z. Atau dapat diinterpretasikan bahwa semakin tinggi nilai X2 maka Z akan semakin meningkat pula. Peningkatan satu satuan X2 akan meningkatkan Z sebesar 22,1%. Berdasarkan perhitungan dengan menggunakan bootstrap atau resampling, dimana hasil uji koefisien estimasi X2 terhadap Z hasil bootstrap adalah sebesar 0,220 dengan nilai t hitung 1,922 dan standar deviasi 0,115. Maka nilai p value adalah 0,055>0,05 sehingga terima H0 atau yang berarti pengaruh langsung X2 terhadap Z tidak bermakna atau tidak signifikan secara statistik.
Direct Effects atau Pengaruh Langsung Y Terhadap Z
Besarnya koefisien parameter untuk variabel Y terhadap Z sebesar 0,320 yang berarti terdapat pengaruh positif Y terhadap Z. Atau dapat diinterpretasikan bahwa semakin tinggi nilai Y maka Z akan semakin meningkat pula. Peningkatan satu satuan Y akan meningkatkan Z sebesar 32,0%. Berdasarkan perhitungan dengan menggunakan bootstrap atau resampling, dimana hasil uji koefisien estimasi Y terhadap Z hasil bootstrap adalah sebesar 0,306 dengan nilai t hitung 3,339 dan standar deviasi 0,096. Maka nilai p value adalah 0,001<0,05 sehingga terima H1 atau yang berarti pengaruh langsung Y terhadap Z bermakna atau signifikan secara statistik.
Bootstrapping PLS SEM Indirect Effects
Hasil dari analisis indirect effects bootstrapping PLS SEM adalah sebagai berikut:
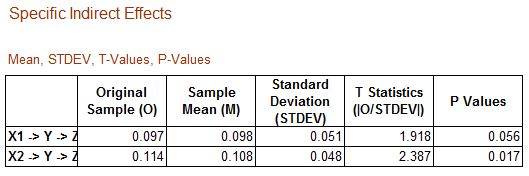
Cara interpretasi pada indirect effects hasil bootstrapping PLS SEM tidak jauh beda dengan interpretasi direct effect bootstrapping PLS SEM.
Indirect Effects atau Pengaruh Tidak Langsung X1 Terhadap Z Melalui Y
Besarnya koefisien parameter untuk variabel X1 terhadap Z melalui Y sebesar 0,097 yang berarti terdapat pengaruh tidak langsung yang positif X1 terhadap Z melalui Y. Atau dapat diinterpretasikan bahwa semakin tinggi nilai X1, maka Z melalui Y akan semakin meningkat pula. Peningkatan satu satuan X1 akan meningkatkan Z melalui Y sebesar 9,7%. Berdasarkan perhitungan dengan menggunakan bootstrap atau resampling, dimana hasil uji koefisien estimasi X1 terhadap Z melalui Y hasil bootstrap adalah sebesar 0,098 dengan nilai t hitung 1,918 dan standar deviasi 0,051. Maka nilai p value adalah 0,056>0,05 sehingga terima H0 atau yang berarti pengaruh tidak langsung X1 terhadap Z melalui Y adalah tidak bermakna atau tidak signifikan secara statistik.
Indirect Effects atau Pengaruh Tidak Langsung X2 Terhadap Z Melalui Y
Besarnya koefisien parameter untuk variabel X2 terhadap Z melalui Y sebesar 0,114 yang berarti terdapat pengaruh tidak langsung yang positif X2 terhadap Z melalui Y. Atau dapat diinterpretasikan bahwa semakin tinggi nilai X2, maka Z melalui Y akan semakin meningkat pula. Peningkatan satu satuan X2 akan meningkatkan Z melalui Y sebesar 11,4%. Berdasarkan perhitungan dengan menggunakan bootstrap atau resampling, dimana hasil uji koefisien estimasi X2 terhadap Z melalui Y hasil bootstrap adalah sebesar 0,108 dengan nilai t hitung 2,387 dan standar deviasi 0,048. Maka nilai p value adalah 0,017<0,05 sehingga terima H1 atau yang berarti pengaruh tidak langsung X2 terhadap Z melalui Y adalah bermakna atau signifikan secara statistik.
Bootstrapping PLS SEM Total Effects
Hasil analisis total effects bootstrapping PLS SEM adalah sebagai berikut:

Oleh karena perantara X1 dengan Y, X2 dengan Y dan Y dengan Z adalah tidak ada, maka total effectnya adalah sama dengan direct effectnya. Sehingga dalam hal ini tidak akan dibahas lebih jauh. Akan kita jelaskan yang mana hanya ada variabel perantaranya yaitu pengaruh total X1 terhadap Z dan pengaruh total X2 terhadap Z.
Total Effects atau Pengaruh Total X1 Terhadap Z
Besarnya koefisien parameter untuk variabel X1 terhadap Z (jumlah pengaruh langsung dan tidak langsung melalui Y) sebesar 0,450 yang berarti terdapat pengaruh total yang positif X1 terhadap Z. Atau dapat diinterpretasikan bahwa semakin tinggi nilai X1, maka Z melalui Y dan tidak melalui Y, akan semakin meningkat pula. Peningkatan satu satuan X1 akan meningkatkan Z sebesar 45,0%. Berdasarkan perhitungan dengan menggunakan bootstrap atau resampling, dimana hasil uji koefisien estimasi X1 terhadap Z hasil bootstrap adalah sebesar 0,467 dengan nilai t hitung 4,135 dan standar deviasi 0,109. Maka nilai p value adalah 0,000<0,05 sehingga terima H1 atau yang berarti pengaruh total X1 terhadap Z adalah bermakna atau signifikan secara statistik.
Total Effects atau Pengaruh Total X2 Terhadap Z
Besarnya koefisien parameter untuk variabel X2 terhadap Z (jumlah pengaruh langsung dan tidak langsung melalui Y) sebesar 0,335 yang berarti terdapat pengaruh total yang positif X2 terhadap Z. Atau dapat diinterpretasikan bahwa semakin tinggi nilai X2, maka Z melalui Y dan tidak melalui Y, akan semakin meningkat pula. Peningkatan satu satuan X2 akan meningkatkan Z sebesar 33,5%. Berdasarkan perhitungan dengan menggunakan bootstrap atau resampling, dimana hasil uji koefisien estimasi X2 terhadap Z hasil bootstrap adalah sebesar 0,328 dengan nilai t hitung 2,489 dan standar deviasi 0,135. Maka nilai p value adalah 0,013<0,05 sehingga terima H1 atau yang berarti pengaruh total X2 terhadap Z adalah bermakna atau signifikan secara statistik.
Bootstrapping PLS SEM Outer Loading
Hasil analisis Bootstrapping pada Outer Loading adalah sebagai berikut:

Berdasarkan gambar tabel hasil bootstrapping PLS SEM terhadap Outer Loading diatas, dapat dilihat bahwasanya semua indikator mempunyai nilai p value <0,05. Sehingga dapat disimpulkan bahwasanya semua indikator berdasarkan nilai outer loading adalah signifikan. Hal tersebut dapat memberikan kesimpulan bahwasanya semua indikator telah valid secara convergen berdasarkan penilaian bootstrapping terhadap outer loading.
Bootstrapping PLS SEM Outer Weight
Hasil analisis Bootstrapping pada Outer Weight adalah sebagai berikut:
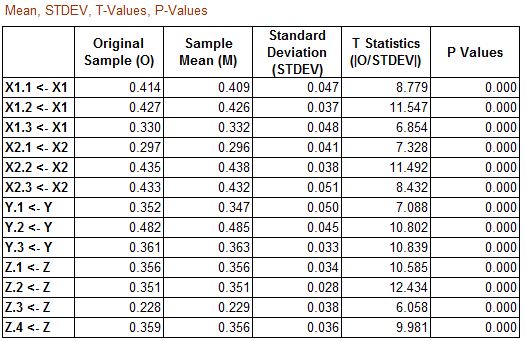
Berdasarkan gambar tabel hasil bootstrapping PLS SEM terhadap Outer Weight diatas, dapat dilihat bahwasanya semua indikator mempunyai nilai p value <0,05. Sehingga dapat disimpulkan bahwasanya semua indikator berdasarkan nilai outer weight adalah signifikan. Hal tersebut dapat memberikan kesimpulan bahwasanya semua indikator telah valid secara convergen berdasarkan penilaian bootstrapping terhadap outer weight.
Kesimpulan PLS SEM Pada SMARTPLS
Berdasarkan serangkaian analisis yang telah dilakukan pada artikel ini dan artikel-artikel sebelumnya, telah kita dapatkan berbagai hasil yang bermanfaat. Antara lain: Validitas dan Reliabilitas menggunakan outer loading dan outer weight beserta signifikansinya, Validitas Convergen, Reliabilitas Butir dan Konstruk, Nilai R Square dan Adjusted R Square, F Square, Direct Effects beserta signifikansinya, Indirect Effects beserta signifikansinya dan Total Effects beserta signifikansinya.
Hingga pada bagian artikel tentang analisis bootstrapping PLS SEM metode basic ini, maka sudah banyak yang kita pelajari dan dapat kita ambil manfaatnya. Maka untuk selanjutnya, apa yang masih belum kita dapatkan, akan kita bahas dalam artikel selanjutnya yaitu melalui artikel kami yang berjudul: Bootstrapping Complete PLS SEM dan Blindfolding. Jangan lupa baca artikel tersebut.
Tetap bersama kami, Anwar Hidayat dalam www.statistikian.com. PLS SEM menjadi mudah bersama kami. Salam sejahtera.
Daftar Pustaka Bootstrapping PLS SEM
Davison, A. C., and Hinkley, D. V. (1997). Bootstrap Methods and Their Application, Cambridge University Press: Cambridge.
Efron, B., and Tibshirani, R. J. (1993). An Introduction to the Bootstrap, Chapman Hall: New York.
G. David Garson and Statistical Associates Publishing (2016). PARTIAL LEAST SQUARES (PLS-SEM). School of Public & International Affairs North Carolina State University.
Ghozali I. dan Latan H. 2015. Partial Least Squares Konsep, Teknik dan Aplikasi Menggunakan Program SmartPLS 3.0. Ed. Ke-2. Badan Penerbit Universitas Diponegoro, Semarang.
Henseler J., Ringle C.M., dan Sarstedt M. 2015. A new criterion for assessing discriminant validity in variance-based structural equation modeling. Journal of the Academy of Marketing Science. Vol. 43 : 115 – 135.
Memon, M. A., Ting, H., Ramayah, T., Chuah, F., & Cheah, J. H. (2017), “A review of the methodological misconceptions and guidelines related to the application of structural equation modeling: A Malaysian scenario”, Journal of Applied Structural Equation Modeling, Vol. 1 No. 1, pp. i-xiii.
Sarstedt M., Ringle C.M., dan Hair J.F. 2017. Partial Least Square Structural Equation Modeling. Dalam : Homburg C., Klarmann M., Vomberg A. (eds) Handbook of Marketing Research. Springer, Cham.
Sekaran U. dan Bougie R. 2016. Research Methods for Business. 7 th ed. John Wiley & Sons Ltd, Chichester.
Wold, Herman (1985). Partial least squares, Pp. 581-591 in Samuel Kotz and Norman L. Johnson, eds., Encyclopedia of statistical sciences, Vol. 6, New York: Wiley, 1985.
Wong K.K. 2013. Partial Least Squares Structural Equation Modeling (PLS-SEM) Techniques Using SmartPLS. Marketing Bulletin. Vol.24: Technical Note1.
Zhao X., Lynch J.G., dan Chen Q. 2010. Reconsidering Baron and Kenny: Myths and Truths about Mediation Analysis. Journal of Consumer Research. Vol. 37 : 197 – 206.
Referensi Lengkap Bootstrapping PLS SEM: https://www.smartpls.com/documentation/algorithms-and-techniques/bootstrapping













Assalamualaikum wr.wb. pak saya mahasiswa mau brtnya mengenai metode PLS, apakah dengan menggunakan aplikasi PLS yg student hasil outputnya dapat di copy ke word? Terimakasih
Tidak bisa