ANOVA R Studio Lengkap Dengan Asumsi dan Post Hoc. Tutorial, Contoh

Tutorial Uji ANOVA Menggunakan Aplikasi R Studio Lengkap Dengan Uji Asumsi dan Post Hoc

Uji ANOVA atau Analysis of Variance Test adalah Uji statistik yang digunakan untuk menilai pengaruh kelompok atau perlakuan terhadap variabel kuantitatif. Analisis yang bisa digunakan pada penelitian eksperimen tersebut dapat dilakukan menggunakan berbagai aplikasi, salah satunya adalah R Studio. Maka dalam kesempatan ini kami akan jelaskan Tutorial Uji ANOVA R Studio. Tutorial ini akan menjelaskan contoh dan cara melakukan analisis ANOVA dengan menggunakan aplikasi R Studio yang tentunya merupakan aplikasi komputasi gratis atau open source namun sangat powerfull.

Aplikasi R Studio disini dapat mengerjakan berbagai perhitungan untuk uji ANOVA mulai dari perhitungan deskriptive, uji asumsi (uji normalitas dan homogenitas), uji ANOVA itu sendiri serta post hoc test atau uji lancut pasca ANOVA seperti misalnya Tukey HSD.

Selain itu aplikasi R Studio ni juga dapat menampilkan berbagai grafik yang diperlukan dalam kaitannya untuk uji ANOVA seperti grafik mean atau rata-rata, grafik normal QQ untuk uji normalitas dan grafik box plot untuk menilai homogenitas variance serta adanya outlier.

Langkah-langkah Uji ANOVA dengan R Studio

Langkah-langkah yang dilakukan pada Analisis ANOVA dengan R Studio adalah sebagai berikut:

1. Persiapkan Data Tabulasi misalnya dalam format Excel (.xlsx atau .csv)
2. Buka aplikasi R Studio
3. Impor data dari excel atau csv ke R Studio
4. Cek kesesuaian data
5. Install package yang dibutuhkan untuk analisis ANOVA R Studio
6. Lakukan Uji Deskriptif
7. Uji ANOVA dengan menggunakan perintah R Studio
8. Uji homogenitas
9. Uji normalitas dan deteksi outlier
10. Jika memenuhi semua asumsi lakukan interpretasi langsung
11. Jika ada outlier lakukan eliminasi atau treatment lainnya
12. Jika tidak memenuhi asumsi normalitas lakukan treatment
13. Jika tidak memenuhi asumsi homogenitas lakukan uji ANOVA yang robust
14. Jika hasil uji ANOVA dengan R Studio hasilnya signifikan maka lakukan uji Post Hoc
15. Jika tidak memenuhi asumsi homogenitas, Post Hoc yang digunakan pilih yang robust
16. Jika semua asumsi tidak dapat terpenuhi dapat menggunakan alternatif uji non-parametris yaitu uji Kruskall Wallis.

Demikian diatas adalah langkah-langkah yang harus dilakukan oleh anda saat melakukan uji ANOVA menggunakan aplikasi R Studio.

Dalam penjelasan langkah-langkah analisis ANOVA dalam r studio di atas disebutkan perlunya uji asumsi homogenitas dan normalitas serta uji post hoc. Agar tutorial di bawah ini nanti dapat dipahami lebih mudah bagi anda para pembaca, maka kiranya penting untuk review kembali tentang uji ANOVA. Atau anda bisa langsung saja baca kembali artikel kami yang telah membahas lebih jauh tentang apa itu uji ANOVA. Silahkan baca artikel kami yang berjudul Uji ANOVA.

Asumsi Uji ANOVA

Uji ANOVA memerlukan asumsi atau prasyarat agar hasil analisisnya valid untuk digunakan. Asumsi tersebut antara lain: Nomalitas dan homogenitas.

Asumsi Normalitas Pada ANOVA

Asumsi normalitas pada ANOVA adalah pada residual yaitu selisih antara Y Prediksi dengan Y Aktual. Tepatnya residual dapat dihitung sebagai berikut: Y Aktual – Y Prediksi. Dimana Y Aktual adalah Y sesungguhnya atau kenyataan. Sedangkan Y prediksi adalah Y hasil persamaan ANOVA. Apa persamaan ANOVA? Silahkan baca artikel kami tentang Uji ANOVA. Asumsi ini mensyaratkan bahwa residual harus berdistribusi normal.

Jika asumsi ini dilanggar maka dapat dilakukan treatment atau solusi antara lain: Trimming yaitu mengeliminir sampel atau observasi yang merupakan data extreme atau sebagai outlier (data pencilan). Cara lainnya adalah dengan melakukan winsorizing dan cara bootstrapping.

Alternatif lainnya jika asumsi normalitas pada ANOVA ini dilanggar yaitu menggunakan uji non parametris untuk uji beda k sampel bebas yaitu uji Kruskall Wallis.

Adapun analisis normalitas pada residual ANOVA yang sering digunakan adalah grafik Normal QQ dan Shapiro Wilk.

Mengapa menggunakan shapiro wilk dalam uji normalitas pada ANOVA dengan R Studio? Sebab biasanya pada ANOVA, jumlah observasi sedikit dimana kurang dari 50 sampel atau observasi. Dan kelebihan Shapiro Wilk adalah bagus dan efektif untuk jumlah sampel kecil kurang dari 50.

Asumsi Homogenitas Pada ANOVA

Homogenitas dapat diartikan ialah kesamaan variance antara kedua kelompok data atau antara beberapa kelompok data. Dalam hal ini, kelompok data yang dimaksud adalah kelompok atau kategori dalam variabel bebas. Biasanya dalam analisis ANOVA yang sering digunakan untuk analisis eksperimen, kelompok tersebut adalah kelompok perlakuan atau kelompok kontrol. Misalnya ada 3 kelompok, yaitu kelompok kontrol, eksperimen 1 dan eksperimen 2.

Variance yang dimaksud disini adalah kuadrat dari standar deviasi atau simpangan baku. Dikatakan homogen jika variance antar kelompok data tersebut tidak berbeda secara nyata. Analisis yang biasa digunakan adalah uji Levene, Fisher F dan Bartlett.

Penjelasan dan contohnya secara adalah sebagai berikut di bawah ini:

Contoh Tutorial One Way ANOVA dengan R Studio

Uji ANOVA sebagai analisis mempunyai beberapa jenis berdasarkan jumlah variabel bebasnya, yaitu antara lain One Way ANOVA, Two Way ANOVA dan Multi Way ANOVA.

Dalam kesempatan ini akan kita pelajari dulu cara melakukan uji One Way ANOVA dengan R Studio. Artinya dalam tutorial ini kita akan menggunakan 1 variabel bebas saja.

Contoh Uji ANOVA R Studio dalam tutorial kali ini akan menggunakan judul yaitu: “Pengaruh Metode Pembelajaran Terhadap Nilai Ujian matematika pada siswa kelas VII.”

Berdasarkan judul diatas, maka sebagai variabel bebas adalah Metode Pembelajaran. Dalam hal ini kita akan menggunakan 4 kelompok atau perlakuan yaitu kelompok Kontrol artinya kelompok tanpa adanya intervensi. Sedangkan kelompok perlakuan ada 3 kelompok yaitu Eksperimen 1 (exp1), Eksperimen 2 (exp2) dan Eksperimen 3 (exp3). Ketiga kelompok tersebut merupakan jenis-jenis perlakuan yang diberikan.

Sebagai subjek penelitian adalah siswa kelas VII yang mana tiap kelompok diambil sampel sejumlah 10 orang atau 10 responden. Jadi jumlah observasi dalam analisis ANOVA R Studio ini adalah sejumlah 4 x 10 = 40 observasi.

Untuk mempermudah para pembaca mempelajari tutorial ANOVA dengan R Studio ini, silahkan anda bisa download file kerja dalam format excel yang digunakan dalam tutorial ini DISINI.

Persiapkan Data Tabulasi

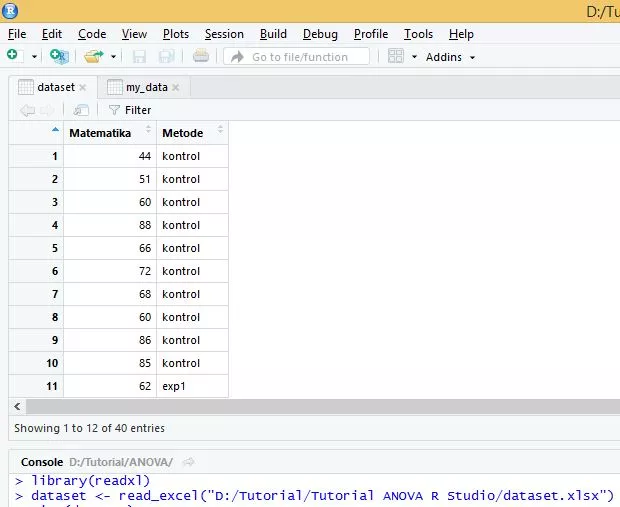
Silahkan buka aplikasi excel anda. Buat data sebagai berikut:

Pada gambar diatas ada 2 kolom yaitu Matematika dan Metode. Dimana sebagai variabel terikat atau dependent variable adalah Matematika. Sedangkan Metode sebagai perlakuan merupakan variabel bebas atau independent variable. Metode mempunyai 4 kelompok yaitu “kontrol”, “exp1”, “exp2” dan “exp3” sebagai jenis perlakuan.

Jadi berdasarkan contoh tabulasi diatas dapat kita pahami bahwa hipotesis yang dibentuk dalam analisis ini adalah: Apakah ada perbedaan Nilai Ujian Matematika antar kelompok perlakuan. Jika jawaban hipotesis ANOVA adalah menolak H0 maka berarti ada perbedaan signifikan atau nyata yang dapat disimpulkan bahwa Metode Pembelajaran memberikan pengaruh yang bermakna terhadap nilai ujian matematika Siswa kelas VII.

Selanjutnya dilakukan Post Hoc Test pasca ANOVA jika terdapat perbedaan Signifikan. Tujuan Uji Post Hoc ini untuk menilai antar kelompok mana yang berbeda secara signifikan. Apakah antara kelompok kontrol dengan exp1? kontrol dengan exp2, exp3 ataukah exp1 dengan exp2, exp3 dan apakah antara exp2 dengan exp3.

Buka Aplikasi R Studio dan Impor Data Tabulasi ANOVA Dari Excel ke R Studio

Buka aplikasi R Studio anda kemudian pada jendela kanan atas anda klik menu “import dataset.”

Selanjutnya akan tampil jendela pencarian file dalam komputer kita, yaitu seperti gambar di bawah ini:

Jika langkah anda benar maka seharusnya di dalam jendela console R Studio, akan tampil kode mirip sebagai berikut:

# Impor data dari excel ke r-studio
library(readxl)
dataset <- read_excel("D:/Tutorial/Tutorial ANOVA R Studio/dataset.xlsx")
View(dataset)

Label “D:/Tutorial/Tutorial ANOVA R Studio/dataset.xls” merupakan lokasi file dataset excel anda yang mana dalam tutorial ini kami beri nama file dataset.xlsx.

Membuat Array Data Untuk Analisis Selanjutnya

Caranya ketikkan berikut pada console:

# Memberi nama data
my_data <- dataset

my_data merupakan name atau nama array data yang akan digunakan untuk analisis selanjutnya.

Cek Data

Untuk memastikan data sudah benar baik kesesuaian jumlah data, jumlah perlakuan atau variabel bebas dan jumlah data variabel terikat maka kita lakukan check ulang sebagai berikut:

Pada console ketikkan:

# Menampilkan data dan cek data
set.seed(1234)
dplyr::sample_n(my_data, 40)

my_data merupakan array data yang kita gunakan. Dan nilai 40 adalah jumlah sampel.

Jika langkah anda benar maka akan tampil sebagai berikut:

# A tibble: 40 x 2
Matematika Metode
<dbl> <chr>
1 76 exp2
2 90 exp1
3 87 exp2
4 96 exp3
5 86 kontrol
6 66 kontrol
7 96 exp3
8 88 kontrol
9 51 kontrol
10 68 kontrol
# ... with 30 more rows

Mengurutkan Data

Agar data urut per kelompok Metode mulai dari kelompok kontrol, exp1, exp2 dan exp3 maka dilakukan sorying menggunakan perintah sebagai berikut:

# Mengurutkan atau shorting data per-eksperimen
levels(my_data$Metode)
my_data$Metode <- ordered(my_data$Metode,
levels = c("kontrol", "exp1", "exp2", "exp3"))

Keterangan dalam kode perintah ANOVA R Studio diatas adalah:

my_data adalah array data yang digunakan. Metode adalah variabel bebas dimana ada 4 kelompok seperti yang tertera dalam kode "levels = c("kontrol", "exp1", "exp2", "exp3"))"

Uji Deskriptif

Selanjutnya anda lakukan uji deskriptif untuk menilai rata-rata atau mean Matematika pada tiap-tiap Metode Pembelajaran.

# Descriptive Test
library(dplyr)
group_by(my_data, Metode) %>%
summarize(
count = n(),
mean = mean(Matematika, na.rm = TRUE),
sd = sd(Matematika, na.rm = TRUE)
)

Kode diatas artinya:

library(dplyr) adalah perintah memanggil perpustakaan atau library yang akan digunakan untuk analisis selanjutnya termasuk analisis deskiptif pada analisis ANOVA R Studio. my_data adalah array data dan Metode adalah variabel bebas. Sedangkan matematika adalah variabel terikat. Count adalah jumlah sampel. Mean adalah rata-rata dan sd adalah standar deviasi atau simpangan baku.

Jika benar langkah anda maka akan tampil seperti berikut ini:

# A tibble: 4 x 4
Metode count mean sd

1 kontrol 10 68 15.0
2 exp1 10 75.8 10.4
3 exp2 10 82 5.64
4 exp3 10 94.3 4.72


Berdasarkan output diatas, dapat diartikan misalnya sebagai berikut: Kelompok kontrol terdiri dari 10 observasi dimana nilai rata-ratanya adalah 68 dengan simpangan baku sebesar 15. Diantara 4 kelompok tersebut, rata-rata tertinggi adalah pada kelompok exp1 yaitu dengan nilai rata-rata 94,3. Sedangkan rata-rata terendah adalah pada kelompok kontrol yaitu dengan nilai rata-rata sebesar 15,0.

Dengan hasil analisis deskriptive diatas, memberikan gambaran bahwa nilai Matematika antar kelompok saling berbeda satu sama lainhya. Selanjutnya apakah perbedaan tersebut bermakna atau signifikan secara statistik? Maka Uji ANOVA R Studio akan menjawab pertanyaan tersebut.

Install Package Untuk Plot atau Grafik

Ketikkan:

# Install Package ANOVA via ICRAN
# Harus Koneksi Internet
install.packages("ggpubr")

Tampilkan Box Plot Masing-masing Kelompok

Ketikkan perintah sebagai berikut:

# Menampilkan Box plots
# Box plots
# ++++++++++++++++++++
# Plot Matematika by Metode and color by Metode
library("ggpubr")
ggboxplot(my_data, x = "Metode", y = "Matematika",
color = "Metode", palette = c("#00AFBB", "#E7B800", "#FC4E07", "#00FF00"),
order = c("kontrol", "exp1", "exp2", "exp3"),
ylab = "Matematika", xlab = "Metode")

Tampilan grafik tersebut adalah sebagai berikut:

Berdasarkan box plot ANOVA R Studio diatas dapat kita perhatikan bahwa terdapat perbedaan rata-rata Matematika antar kelompok Metode Pembelajaran dimana pada kelompok perlakuan exp3 adalah yang paling tinggi.

Sedangkan bentuk box plot diatas juga menunjukkan bahwa variance antar kelompok relatif sama. Namun pada exp3 terdapat data pencilan atau outlier.

Tampilkan Box Plot Mean Standar Error Untuk Menilai Perbedaan Rata-rata.

Ketikkan perintah sebagai berikut:

# Menampilkan Box plots dengan nilai MEAN dan Standar Error
# Mean plots
# ++++++++++++++++++++
# Plot weight by group
# Add error bars: mean_se
# (other values include: mean_sd, mean_ci, median_iqr, ....)
library("ggpubr")
ggline(my_data, x = "Metode", y = "Matematika",
add = c("mean_se", "jitter"),
order = c("kontrol", "exp1", "exp2", "exp3"),
ylab = "Matematika", xlab = "Metode")

Maka tampilan plot adalah sebagai berikut:

Berdasarkan plot diatas dapat kita nilai bahwa rata-rata nilai Matematika kelompok exp3 paling tinggi disusul exp2 kemudian exp1. Sedangkan kelompok yang terendah adalah kelompok kontrol.

Hitung Uji F ANOVA dengan R Studio

Berikut adalah langkah utama kita dalam melakukan analisis One Way ANOVA dengan R Studio yaitu akan kita lakukan uji F ANOVA.

Caranya adalah ketikkan perintah pada console sebagai berikut:

# Analisis ANOVA -> analysis of variance. -
# Jika data memenuhi asumsi homogenitas variances
res.aov <- aov(Matematika ~ Metode, data = my_data)
# Summary of the analysis
summary(res.aov)

Perintah diatas adalah perintah ANOVA pada R Studio jika seandainya asumsi normalitas dan homogenitas terpenuhi. Hasilnya adalah sebagai berikut:

Hasil uji F ANOVA diatas menunjukkan bahwa: DF adalah degree of freedom yaitu DF1 atau numerator adalah jumlah kelompok 4 – 1 = 3. DF2 atau denumerator yaitu observasi – DF1 = 40 – 4 = 36. Nilai Mean Square Metode adalah 1234 dengan F Hitung sebesar 12,72 maka nilai signifikansi atau p value uji F ANOVA adalah sebesar 8.04e-06 atau 8,04 x 10 pangkat -06 yang mana nilai p value tersebut < 0,05.

Oleh karena P Value < 0,05 maka dapat disimpulkan bahwa menolak H0 yang artinya Metode berpengaruh signifikan dalam mempengaruhi Nilai Ujian Matematika pada siswa kelas VII. Atau dapat diartikan pula bahwa terdapat perbedaan signifikan nilai ujian matematika siswa kelas VII antar kelompok metode pembelajaran.

Oleh karena uji F Anova menggunakan aplikasi R Studio ini menunjukkan bahwa terima H1 maka selanjutnya dapat dilanjutkan uji lanjut atau Post Hoc Test.

Post Hoc Test pada R Studio

Dalam utorial ini, uji post hoc yang akan kita lakukan adalah Tukey HSD dan Pairwise T Test dimana post hoc test tersebut digunakan untuk uji lanjut pasca ANOVA jika memenuhi asumsi homogenitas.

Post Hoc Tukey HSD

Perintah melakukan Post Hoc Tukey HSD pada R Studio adalah sebagai berikut:

# Post Hoc Tukey HSD jika memenuhi asumsi homogenitas variances
TukeyHSD(res.aov)

Hasilnya sebagai berikut:

Nilai “diff” adalah nilai perbedaan rata-rata kedua kelompok. Nilai”lwr” adalah nilai batas bawah perbedaan rata-rata dalam selang kepercayaan 95%. Dan “upr” adalah batas atasnya. Nilai “p adj” adalah nilai p value Post Hoc Tukey HSD. Jika nilai p value < 0,05 maka menolak H0 yang artinya perbedaan tersebut signifikan.

Berdasarkan analisis Tukey HSD diatas, misalnya perbedaan rata-rata nilai ujian Matematika antara kelompok exp1 dengan kelompok kontrol  adalah sebesar 7,8 dimana dalam selang kepercayaan 95%, batas bawah dan atas adalah antara -4.0619256 sd 19.66193 dengan p value 0.3036051>0,05 maka menerima H0. Artinya perbedaan rata-rata nilai ujian Matematika antara kelompok exp1 dengan kelompok kontrol  adalah tidak signifikan secara statistik dalam selang kepercayaan 95%.

Post Hoc Pairwise T Test

Perintah melakukan Post Hoc Pairwise T Test pada R Studio adalah sebagai berikut:

# Post pairwise t test dengan p value adjusted oleh Benjamini-Hochberg method. -
# jika memenuhi asumsi homogenitas variances
pairwise.t.test(my_data$Matematika, my_data$Metode,
p.adjust.method = "BH")

Catatan: Analisis post hoc diatas menggunakan pairwise t test dengan koreksi p value oleh Benjamini-Hochberg yang digunakan jika asumsi homogenitas terpenuhi.

Hasilnya adalah sebagai berikut:

Cara interpretasi Post Hoc ANOVA diatas adalah: nilai yang tertera adalah nilai p value yang kemudian dibandingkan dengan batas kritis 0,05. Jika nilainya < 0,05 maka menolak H0 yang artinya terdapat perbedaan rata-rata yang signifikan.

Misalnya perbedaan rata-rata nilai ujian Matematika antara kelompok exp2 dengan kelompok kontrol  mendapatkan nilai p value sebesar 0,0061<0,05 maka menolak H0. Artinya perbedaan rata-rata nilai ujian Matematika antara kelompok exp2 dengan kelompok kontrol  adalah signifikan secara statistik dalam selang kepercayaan 95%.

Uji Asumsi Homogenitas pada ANOVA R Studio

Ada 2 cara uji homogenitas ANOVA dalam R Studio ini, yaitu menggunakan grafik atau plot dan menggunakan uji levene. Grafik yang digunakan adalah scatter plot antara residual dengan y prediksi.

Scatter plot antara residual dengan y prediksi

Caranya sebagai berikut:

# Uji homogenitas variances menggunakan grafik
plot(res.aov, 1)

Scatter Plot diatas menunjukkan bahwa ada beberapa outlier yaitu sampel nomor 1, 4 dan 9. Dengan adanya outlier dalam diagram tersebut dapat menunjukkan bahwa terdapat heterogenitas sehingga asumsi homogenitas variance tidak terpenuhi. Namun untuk memastikan akan kita uji menggunakan Levene Test.

Levene Test

Cara melakukan Levene test pada R Studio adalah sebagai berikut:

# Uji homogenitas variances menggunakan levene test
library(car)
leveneTest(Matematika ~ Metode, data = my_data)

Hasilnya sebagai berikut:

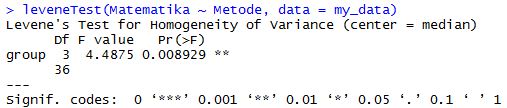
Hasil Levene Test diatas menunjukkan bahwa nilai p value sebesar 0,008929 dimana nilainya kurang dari 0,05 sehingga menolak H0 yang artinya variance antar kelompok berbeda secara nyata. Oleh karena variance berbeda secara nyata atau signifikan maka dapat disimpulkan bahwa heterogen yang artinya tidak memenuhi asumsi homogenitas.

Terjadinya pelanggaran asumsi homogenitas pada ANOVA dengan R Studio ini memberikan konsekuensi sebagai berikut:

1. Uji F ANOVA R Studio dikoreksi menggunakan analisis ANOVA yang robust atau kebal terhadap pelanggaran asumsi homogenitas.
2. Uji post Hoc pasca ANOVA R Studio dikoreksi menggunakan analisis post Hoc yang robust atau kebal terhadap pelanggaran asumsi homogenitas.

Uji F ANOVA Robust Pelanggaran Homogenitas

Cara melakukan Uji F ANOVA yang Robust terhadap Pelanggaran Homogenitas pada R Studio adalah sebagai berikut:

# ANOVA test jika asumsi homogenitas variances tidak terpenuhi
oneway.test(Matematika ~ Metode, data = my_data)

Hasilnya akan tampak seperti di bawah ini:

Hasil uji F ANOVA Robust diatas menunjukkan bahwa:

DF adalah degree of freedom yaitu DF1 atau numerator adalah jumlah kelompok 4 – 1 = 3. DF2 atau denumerator yang telah adjusted adalah sebesar 18,874. Nilai F Hitung sebesar 18,483 maka nilai signifikansi atau p value uji F ANOVA adalah sebesar 7.626e-06 atau 7,626 x 10 pangkat -06 yang mana nilai p value tersebut < 0,05.

Oleh karena P Value < 0,05 maka dapat disimpulkan bahwa menolak H0 yang artinya Metode berpengaruh signifikan dalam mempengaruhi Nilai Ujian Matematika pada siswa kelas VII. Atau dapat diartikan pula bahwa terdapat perbedaan signifikan nilai ujian matematika siswa kelas VII antar kelompok metode pembelajaran.

Oleh karena uji F Anova Robust menggunakan aplikasi R Studio ini menunjukkan bahwa terima H1 maka selanjutnya dapat dilanjutkan uji lanjut atau Post Hoc Test Robust.

Post Hoc Robust Asumsi Homogenitas

Post Hoc Test yang robust terhadap pelanggaran homogenitas adalah menggunakan pairwise t test untuk variance tidak sama. Berikut caranya:

# Post pairwise t test dengan p value adjusted oleh Benjamini-Hochberg method. -
# jika asumsi homogenitas variances tidak terpenuhi
pairwise.t.test(my_data$Matematika, my_data$Metode,
p.adjust.method = "BH", pool.sd = FALSE)

Hasilnya seperti di bawah ini:

Cara interpretasi Post Hoc ANOVA Robust diatas adalah: nilai yang tertera adalah nilai p value yang kemudian dibandingkan dengan batas kritis 0,05. Jika nilainya < 0,05 maka menolak H0 yang artinya terdapat perbedaan rata-rata yang signifikan.

Misalnya perbedaan rata-rata nilai ujian Matematika antara kelompok exp3 dengan kelompok kontrol  mendapatkan nilai p value sebesar 0,00055<0,05 maka menolak H0. Artinya perbedaan rata-rata nilai ujian Matematika antara kelompok exp3 dengan kelompok kontrol  adalah signifikan secara statistik dalam selang kepercayaan 95%.

Uji Asumsi Normalitas

Cara melakukan uji normalitas pasca uji ANOVA dengan R Studio ada 2 cara, yaitu menggunakan grafik Normal QQ dan menggunakan uji Shapiro Wilk.

Grafik Normal QQ

Cara analisis normalitas mengunakan Normal QQ adalah sebagai berikut:

# Uji Normalitas dengan grafik Normal QQ
plot(res.aov, 2)

Hasilnya adalah seperti diagram berikut:

Berdasarkan Normal QQ diatas, tampak bahwa plot mengikuti garis diagonal sehingga residual berdistribusi normal. Maka analisis ANOVA dengan R Studio ini memenuhi asumsi normalitas. Berikut akan kita pastikan juga menggunakan uji shapiro wilk.

Shapiro Wilk

Cara uji normalitas menggunakan Shapiro Wilk dalam R Studio adalah sebagai berikut:

# Uji Normalitas menggunakan uji Shapiro Wilk
# Extract the residuals
aov_residuals <- residuals(object = res.aov)
# Run Shapiro-Wilk test
shapiro.test(x = aov_residuals)

Hasilnya sebagai berikut:

Berdasarkan hasil analisis diatas, nilai W sebesar 0,98307 dengan nilai p value 0,8009 dimana lebih dari 0,05 sehingga menerima H0 yang artinya Residual berdistribusi normal. Oleh karena residual berdistribusi normal maka uji ANOVA dengan R Studio ini memenuhi asumsi normalitas.

Uji Non Parametris Sebagai Alternatif ANOVA

Jika asumsi homogenitas dan/atau normalitas pada ANOVA tidak terpenuhi maka dapat digunakan uji non parametris sebagai alternatifnya yaitu menggunakan uji Kruskall Wallis.

Cara melakukan uji Kruskall Wallis sebagai alternatif ANOVA menggunakan aplikasi R Studio adalah sebagai berikut:

# Uji Non-parametric sebagai alternatif uji ANOVA
# Sebuah analisis non-parametric sebagai alternative uji ANOVA adalah: -
# Kruskal-Wallis rank sum test, -
# Jika asumsi ANOVA tidak dipenuhi.
kruskal.test(Matematika ~ Metode, data = my_data)

Hasilnya adalah sebagai berikut:

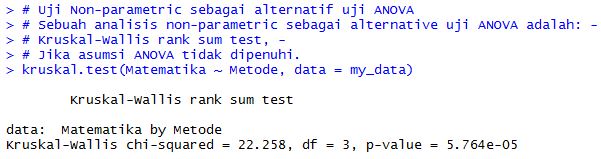
Hasil uji Kruskall Wallis sebagai alternatif uji ANOVA dengan R Studio diatas menunjukkan bahwa:

DF adalah degree of freedom yaitu jumlah kelompok 4 – 1 = 3. Nilai Chi Square Hitung sebesar 22,258 maka nilai signifikansi atau p value uji Kruskall Wallis adalah sebesar 5.764e-05 atau 5,764 x 10 pangkat -05 yang mana nilai p value tersebut < 0,05.

Oleh karena P Value < 0,05 maka dapat disimpulkan bahwa menolak H0 yang artinya Metode berpengaruh signifikan dalam mempengaruhi Nilai Ujian Matematika pada siswa kelas VII. Atau dapat diartikan pula bahwa terdapat perbedaan signifikan nilai ujian matematika siswa kelas VII antar kelompok metode pembelajaran.

Demikian para pembaca sekalian kami telah menjelaskan tutorial cara melakukan uji one way ANOVA dengan R Studio. Semoga artikel tutorial ANOVA R Studio ini bermanfaat bagi orang banyak.