Cara Membaca Hasil Regresi Data Panel Dengan Eviews
Regresi Data Panel telah kita pelajari secara tahap demi tahap menggunakan aplikasi eviews pada artikel-artikel sebelumnya. Saat ini tiba waktunya bagi kita untuk mempelajari bagaimana Cara Membaca Hasil Regresi Data Panel dengan eviews. Untuk menyingkat waktu, marilah kita mulai tutorial ini.
Sebelumnya pastikan bahwa anda telah membaca artikel kami secara serial perihal regresi data panel dengan eviews, yaitu:
- Tutorial Regresi Data Panel dengan Eviews,
- Tutorial Hausman Test dengan Eviews,
- Tutorial Lagrange Multiplier Test dengan Eviews.

Jika anda sudah paham betul tentang langkah-langkah yang telah dijelaskan dalam daftar artikel di atas, sudah saatnya anda bisa masuk dalam tahap menjelaskan atau membaca hasil regresi data panel dengan eviews.
Model Regresi Data Panel
Setelah anda melakukan tahap untuk menentukan metode estimasi yang terbaik dalam regresi data panel, maka tentunya ada tiga pilihan yang akan anda pilih. Yaitu:
- Common Effect atau Pooled Least Square (Panel Least Square),
- Fixed Effect,
- Random Effect.
Oleh karena ada tiga pilihan metode estimasi, maka akan kami jelaskan satu persatu cara membaca output hasil regresi data panel dengan eviews berdasarkan metode estimasi yang ada. Berikut kami mulai dengan common effect.
Cara Membaca Hasil Regresi Data Panel Model Common Effect
Model Common Effect
Model Common effect adalah model atau metode estimasi paling dasar dalam regresi data panel, dimana tetap menggunakan prinsip ordinary least square atau kuadrat terkecil. Oleh karena itulah, metode ini disebut juga dengan istilah pooled least square. Pada model common effect ini tidak memperhatikan dimensi waktu dan juga dimensi individu atau cross section, sehingga bisa diasumsikan bahwa perilaku dari individu tidak berbeda didalam berbagai kurun waktu.
Jika anda sudah melakukan langkah-langkah yang telah kita pelajari sebelumnya, tentunya akan dihadapkan pada output sebagai berikut:

Berdasarkan output di atas, mari kita jelaskan satu persatu cara membaca hasil regresi data panel dengan eviews.
Ringkasan Hasil Regresi Data Panel Model Common Effects
- Periods Include: Merupakan jumlah periode atau runtut waktu yang dilibatkan dalam analisis. Dimana dalam contoh regresi data panel ini, periode yang digunakan adalah tahun 1968 sampai dengan 1978. Sehingga jumlah tahun yang digunakan dalam analisis adalah sebanyak 19 tahun.
- Cross section Include: Merupakan jumlah cross section atau panel yang dilibatkan dalam analisis. Dimana dalam contoh regresi data panel ini, panel yang digunakan adalah negara yang jumlahnya adalah sebanyak 18 negara.
- Total Panel (Balanced) observations: adalah jumlah observasi yang dilibatkan dalam analisis. Istilah balanced artinya balance, yaitu jumlah waktu (tahun) yang digunakan setiap panel (negara) adalah sama atau konstan. Sehingga perhitungannya adalah 19 x 18 = 342 observasi.
- Kolom Variable: adalah daftar variabel yang dianalisis. Dimana dalam contoh regresi data panel ini menggunakan Y sebagai variabel response. Sedangkan variabel prediktor adalah X1, X2 dan X3. Dan C sebagai residual atau error dari persamaan regresi data panel.
Koefisien Regresi Data Panel Model Common Effects
- Coefficient: adalah koefisien beta regresi data panel sesuai dengan variabel yang ada pada kolom variabel. Nilai koefisien ini digunakan untuk membentuk Persamaan Regresi Data Panel.
- Standar error: adalah Standar Error dari nilai koefisien pada kolom coefficient.
- t-statistics: adalah nilai t parsial regresi data panel sesuai per variabel pada kolom variable. Nilai t ini menunjukkan pengaruh parsial variabel prediktor terhadap variabel response di dalam model regresi data panel.
- Prob: adalah nilai p value atau tingkat signifikansi dari t parsial di kolom t-statistics. Nilai p value ini menunjukkan tingkat signifikansi t parsial dalam rangka menjawab hipotesis uji parsial. Jika nilai p value kurang dari batas kritis, misalnya 0,05 maka jawaban hipotesis adalah menerima H1 atau yang berarti variabel prediktor yang bersangkutan memiliki pengaruh yang bermakna terhadap variabel response secara statistik. Dan sebaliknya jika p value lebih dari batas kritis maka menerima H0 atau yang berarti variabel prediktor yang bersangkutan tidak memiliki pengaruh yang bermakna terhadap variabel response secara statistik.
Persamaan Common Effect
Bentuk persamaan regresi data panel mirip dengan ordinary least square, yaitu:

Keterangan: Untuk i = 1, 2, …., N dan t = 1, 2, ….,T.
Dimana N = Jumlah individu atau cross section dan T adalah jumlah periode waktunya. Dari model ini akan dapat dihasilkan N+T persamaan, yaitu sebanyak T persamaan cross section dan sebanyak N persamaan runtut waktu atau time series.
Jawaban Hipotesis Regresi Data Panel Model Common Effects
- R Square: adalah besarnya pengaruh atau kemampuan variabel prediktor secara simultan dalam menjelaskan variabel response. Jika nilainya lebih dari 0,5 maka kemampuan variabel prediktor kuat dalam menjelaskan variabel response. Sedangkan sebaliknya jika nilainya kurang dari 0,5 maka kemampuan variabel prediktor tidak kuat dalam menjelaskan variabel response. Dalam contoh regresi data panel ini, nilai R Square sebesar 0,9579, yang artinya variabel prediktor sangat kuat dalam menjelaskan variabel response.
- Adjusted R Square: adalah besarnya pengaruh atau kemampuan variabel prediktor secara simultan dalam menjelaskan variabel response dengan memperhatikan standar error. penjelasannya sama dengan R Square namun nilai ini telah terkoreksi dengan standar error.
- F-Statistics: adalah nilai Uji F yang merupakan uji simultan dari regresi data panel. Nilai F ini menunjukkan tingkat signifikansi pengaruh variabel prediktor terhadap variabel response. Untuk menggunakan nilai F ini haruslah dibandingkan dengan F Tabel. Namun untuk memudahkan bisa langsung melihat nilai Prob (F-Statistics).
- Prob (F-Statistics): adalah p value uji F yang merupakan tingkat signifikansi dari nilai F, yaitu untuk menilai pengaruh simultan variabel prediktor terhadap variabel response apakah bermakna secara statistik atau tidak. Jika nilai p value kurang dari batas kritis misalnya 0,05 maka menerima H1 atau yang berarti pengaruh simultan variabel prediktor terhadap variabel response terbukti bermakna secara statistik. Begitu sebaliknya jika nilai p value lebih dari batas kritis maka menerima H0 atau yang berarti pengaruh simultan variabel prediktor terhadap variabel response tidak terbukti bermakna secara statistik.
Demikian di atas adalah penjelasan Cara Membaca Hasil Regresi Data Panel model common effects. Selanjutnya akan kita jelaskan di bawah ini yaitu Cara Membaca Hasil Regresi Data Panel model fixed effects.
Cara Membaca Hasil Regresi Data Panel Model Fixed Effect
Model Fixed Effect
Model Fixed effect berbeda dengan common effect, namun tetap menggunakan prinsip ordinary least square. Asumsi dari pembuatan model yang menghasilkan intersep konstan untuk setiap cross section dan waktu dianggap kurang realistik, maka dibutuhkanlah model yang lebih dapat menangkap adanya perbedaan itu.
Fixed effects mengasumsikan bahwa perbedaan antar individu (cross section) dapat diakomodasi dari perbedaan intersepnya. Agar dapat mengestimasi Fixed Effects Model dengan intersep berbeda antar individu, maka digunakanlah teknik variable dummy. Model estimasi seperti ini sering kali disebut sebagai teknik Least Squares Dummy Variable atau yang disingkat dengan istilah LSDV.
Jika anda sudah melakukan langkah-langkah yang telah kita pelajari sebelumnya, tentunya akan dihadapkan pada output sebagai berikut:
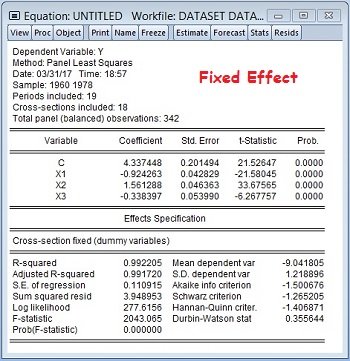
Cara Membaca Hasil Regresi Data Panel Model Fixed Effect sama dengan Cara Membaca Hasil Regresi Data Panel Model Common Effect. Yang membedakan adalah nilainya saja dan bentuk persamaan regresi data panel berdasarkan koefisien beta.
Persamaan Fixed Effect
Persamaan regresi data panel model fixed effects adalah sebagai berikut:
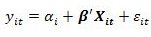
Keterangan: untuk i = 1,2, …., N dan t = 1,2, …., T.
Dimana N = jumlah individu atau cross section dan T = jumlah periode waktunya.
Cara Membaca Hasil Regresi Data Panel Model Random Effect
Model Random Effect
Pada prinsipnya model random effect berbeda dengan common effect dan fixed effect, terutama model ini tidak menggunakan prinsip ordinary least square, melainkan menggunakan prinsip maximum likelihood atau general least square.
Output random effect contohnya adalah sebagai berikut:
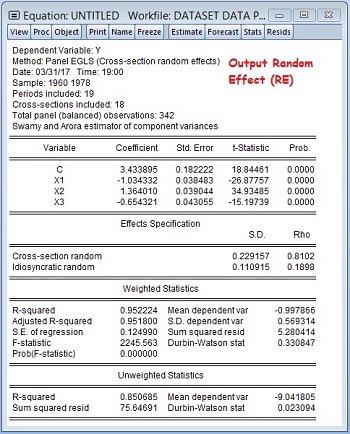
Cara membaca output pada random effect tidak jauh beda dengan common effect ataupun fixed effect. Hanya saja dalam eviews kita akan melihat dua output yaitu weighted dan unweighted. Selain itu juga ada berbagai jenis random effects method yang digunakan, dimana yang paling sering digunakan adalah swamy arora estimator. Namun dalam kesempatan ini kita tidak akan membahas terlalu jauh hal tersebut. Langsung saja kita lihat bentuk persamaan regresi data panelnya.
Persamaan Random Effect
Jika kita menggunakan Fixed Effects melalui teknik LSDV, akan menunjukkan ketidakpastian model yang digunakan. Model random effect ini berguna untuk mengatasi masalah tersebut dengan cara menggunakan variable residual.
Pada model random effect, residual mungkin saling berhubungan antar waktu dan antar individu atau cross section. Oleh karena itu, model ini mengasumsikan bahwa ada perbedaan intersep untuk setiap individu dan intersep tersebut merupakan variable random. Maka di dalam model random effect terdapat dua komponen residual. Yang pertama adalah residual secara menyeluruh dimana residual tersebut merupakan kombinasi dari cross section dan time series. Sedangkan residual yang kedua adalah residual secara individual yang merupakan karakteristik random dari observasi unit ke-i dan tetap sepanjang waktu.
Persamaan regresi data panel model random effects adalah sebagai berikut:

Keterangan: untuk i = 1,2, …., N dan t = 1,2, …., T.
Dimana N = jumlah individu atau cross section dan T = jumlah periode waktunya.
Eit = adalah residual secara menyeluruh dimana residual tersebut merupakan kombinasi dari cross section dan time series.
Ui = adalah residual secara individual yang merupakan karakteristik random dari observasi unit ke-i dan tetap sepanjang waktu.
Demikian di atas adalah penjelasan dari statistikian dalam rangka memahami secara komprehensi atau secara lengkap tentang Cara Membaca Hasil Regresi Data Panel dengan eviews. Semoga bermanfaat.
By Anwar Hidayat
















Setelah diketahui model yang tepat berdasarkan uji hausman test apakah model yang digunakan kembali ke model yang sebelum diuji, fixed atau random ?
Jika hasil Hausman Test terima H1 maka gunakan Fixed Effects (FE). Jika Hausman Test terima H0 maka gunakan Random Effects (RE), namun lebih dulu cek menggunakan Uji Lagrangian Multiplier Test untuk memilih CE ataukah RE.