Penjelasan dan Tutorial Regresi Linear Berganda
Dalam kesempatan ini, saya akan coba menjelaskan tentang Regresi Linear Berganda serta tutorial regresi linear berganda dengan SPSS. Mungkin bisa dibilang artikel ini terlambat saya buat, sebab pada kesempatan lainnya sudah banyak sekali artikel tentang regresi linear berganda dengan berbagai software, seperti minitab, stata dan excel.
Dalam kesempatan ini, saya akan fokus dalam menjelaskan pengertian atau apa itu sebenarnya regresi linear berganda. Serta apa saja asumsi atau syaratnya serta bagaimana cara melakukannya melalui contoh tutorial regresi linear berganda dengan SPSS.
Jadi secara garis besar dalam artikel ini akan ada 2 pokok bahasan, yaitu:
- Penjelasan dan Pengertian Regresi Linear.
- Asumsi Klasik Regresi Linear.
- Contoh Tutorial Regresi Linear dengan SPSS.
Penjelasan Pengertian Regresi Linear Berganda
Regresi Linear Berganda adalah model regresi linear dengan melibatkan lebih dari satu variable bebas atau predictor. Dalam bahasa inggris, istilah ini disebut dengan multiple linear regression.
Pada artikel yang lain, yaitu pada artikel penjelasan berbagai jenis regresi berganda, saya sudah jelaskan perbedaan antara regresi berganda dengan regresi sederhana. Pada dasarnya regresi linear berganda adalah model prediksi atau peramalan dengan menggunakan data berskala interval atau rasio serta terdapat lebih dari satu predictor.
Skala data yang dimaksud diatas adalah pada semua variabel terutama variable terikat. Pada regresi linear, tidak menutup kemungkinan digunakannya data dummy pada variable bebas. Yaitu pada regresi linear dengan dummy.
Perbedaan Regresi Linear Berganda dan Sederhana
Seperti yang sudah saya bahas diatas, dikatakan regresi linear berganda jika jumlah variable bebas atau variabel prediktor lebih dari satu. Sedangkan jika jumlah variable bebas hanya ada satu saja, maka itu yang disebut dengan regresi linear sederhana.
Model regresi linear berganda dilukiskan dengan persamaan sebagai berikut:
Y = α + β1 X2 + β2 X2 + βn Xn + e
Keterangan:
Y = Variabel terikat atau variabel response.
X = Variabel bebas atau variabel predictor.
α = Konstanta.
β = Slope atau Koefisien estimate.

Asumsi Klasik Regresi Linear Berganda
Seperti halnya uji parametris lainnya, maka regresi linear juga mempunyai syarat atau asumsi klasik yang harus terpenuhi. Agar model prediksi yang dihasilkan nantinya bersifat BLUE (Best Linear Unbiased Estimation).
Asumsi klasik pada regresi linear berganda antara lain: Data interval atau rasio, linearitas, normalitas pada residual, non outlier atau tanpa adanya data pencilan (data extreme), homoskedastisitas (Non Heteroskedastisitas), non multikolinearitas dan non autokorelasi.
Data Interval atau rasio.
Skala data semua variable terutama variable terikat adalah interval atau rasio. Asumsi ini tidak perlu diuji, cukup anda pastikan bahwa data yang digunakan adalah data interval atau rasio (numeric atau kuantitatif).
Agar anda paham tentang berbagai skala data, kami sudah membahasnya dalam artikel berjudul jenis data dan pemilihan analisis statistik.
Linearitas
Ada hubungan linear antara variable bebas dengan variable terikat. Asumsi linearitas diuji dengan uji linearitas regresi, misalnya dengan kurva estimasi.
Dengan kurva estimasi kita bisa tentukan ada hubungan linear atau tidak dengan melihat nilai p value linearitas. Jika p value < 0,05 maka terdapat hubungan yang linear antara predictor dan response.
Untuk uji linearitas regresi, kami sudah membahasnya pada artikel yang telah lalu, yaitu artikel linearitas regresi.
Normalitas Residual
Residual adalah beda antara y dengan y prediksi. Y adalah variable terikat, sedangkan y prediksi adalah Y hasil persamaan regresi yang dibuat. Sehingga residual dibangun dengan rumus: y – y prediksi.
Asumsi normalitas pada regresi linear berganda adalah pada residualnya, bukan pada data per variabelnya.
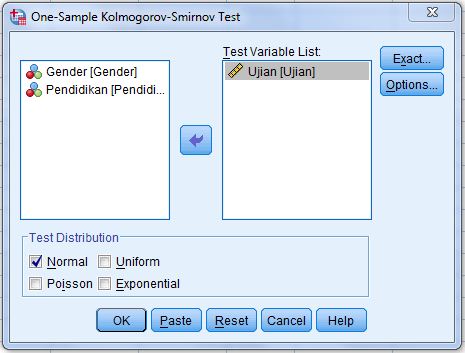
Uji Asumsi normalitas regresi linear dapat diuji dengan berbagai metode uji normalitas, seperti uji Shapiro wilk, lilliefors atau Kolmogorov smirnov, Anderson darling, Ryan joiner, Shapiro francia, Jarque bera, Skewness kurtosis test dan berbagai jenis uji normalitas lainnya.
Berbagai jenis uji normalitas tersebut sudah saya bahas secara tuntas dalam berbagai artikel yang telah saya rilis sebelumnya. Silahkan dipelajari untuk menambah wawasan anda.
Non Outlier
Outlier disebut dengan data pencilan atau data yang nilainya extreme atau lain dari pada yang lainnya. Batasan outlier atau tidak bisa dilihat dari nilai absolut studentized residual. Jika absolut studentized residual > 3 maka sampel atau observasi yang dimaksud menjadi outlier.
Lebih lanjut tentang outlier regresi linear, sudah saya bahas pada artikel tentang Tutorial cara mengatasi outlier dengan SPSS.
Homoskedastisitas
Homoskedastisitas adalah sebuah kondisi dimana varians dari error bersifat konstan atau tetap. Dengan kata lain bahwa varians dari error bersifat identic untuk setiap pengamatan.
Kebalikan dari homoskedastisitas adalah heteroskedastisitas. Model regresi linear yang baik adalah model yang bebas dari kondisi heteroskedastisitas.
Untuk menguji homoskedastisitas pada regresi linear, dapat digunakan uji homoskedastisitas dari glejser, uji park, uji white, spearman heteroskedastisitas, dan masih banyak uji lainnya. Yang tentunya sudah saya bahas pada artikel lainnya terutama pada artikel uji heteroskedastisitas.
Non Multikolinearitas
Multikolinearitas adalah keadaan dimana terdapat interkorelasi atau korelasi kuat antar variable bebas di dalam model. Dinyatakan ada interkorelasi jika korelasi antar variable bebas di dalam model regresi linear berganda > 0,8. Beberapa pakar menggunakan batasan lebih dari 0,9.
Cara lain yang lebih objektif adalah dengan menggunakan nilai variance inflating factor (VIF) dan tolerance. Dikatakan ada multikolinearitas jika nilai VIF > 10 dan/atau nilai tolerance < 0,01.
Untuk lebih jelasnya tentang asumsi multikolinearitas, silahkan baca artikel kami yang berjudul: Tutorial uji multikolinearitas dengan SPSS dan Cara Baca.
Berdasarkan uraian diatas, maka jelas sekali bahwa asumsi multikolinearitas hanya ada dalam regresi linear berganda dan tidak ada pada regresi linear sederhana. Sebab pada regresi linear berganda ada lebih dari satu variabel bebas, sedangkan pada regresi linear sederhana hanya ada satu variable bebas.
Non Autokorelasi
Autokorelasi dapat diartikan bahwa terdapat korelasi antar waktu. Sehingga bisa diartikan dengan mudah bahwa autokorelasi ini sering terjadi pada regresi linear dengan data time series atau runtun waktu. Dan jarang sekali terjadi pada data cross section.
Data runtun waktu ini misalnya data return saham sebuah perusahaan per bulan dari tahun 2012 sd 2017.
Sedangkan data cross section, misalnya data hasil dari kuesioner yang disebarkan pada semua siswa sebuah kelas, dimana hanya diukur satu kali saja.
Uji autokorelasi ini bisa diuji dengan menggunakan nilai Durbin Watson (DW) dan run test. Jika menggunakan uji Durbin Watson, dikatakan tidak ada autokorelasi jika nilai DW hitung > Batas atas DW table dan (4 – DW Hitung) > Batas atas DW Tabel.
Untuk mengenal lebih jauh tentang Durbin Watson table dan uji autokorelasi, silahkan baca artikel kami yang berjudul Pengertian dan Penjelasan Uji Autokorelasi Durbin Watson dengan SPSS.
Kesalahan Persepsi Tentang Asumsi Regresi Linear
Ada beberapa kesalahan klasik yang sering terjadi pada para peneliti yang masih awal belajar untuk meneliti. Terutama yang masih awal berkenalan dengan regresi linear. Yaitu: lebih dulu melakukan uji asumsi klasik baru kemudian melakukan uji regresi linear.
Seharusnya, dari sekian banyak asumsi yang ada dalam regresi linear berganda, hanya asumsi linearitas yang harus dilakukan terlebih dulu. Dan uji linearitas regresi hanya dilakukan jika tujuan dari dibuatnya model regresi adalah untuk membentuk model terbaik.
Sedangkan jika tujuannya untuk sekedar menjawab hipotesis, maka asumsi linearitas ini bisa diabaikan.
Asumsi multikolinearitas bisa dilakukan sebelum uji regresi, sebab yang digunakan adalah data per variable. Sedangkan asumsi yang lainnya haruslah setelah dilakukan uji regresi. Alasannya adalah: uji normalitas, outlier, homoskedastisitas dan autokorelasi menggunakan nilai error atau residual sebagai parameternya.
Software regresi Linear Berganda
Seperti yang sudah saya bahas di awal artikel ini, bahwasanya saya sudah membuat berbagai jenis artikel tentang regresi linear menggunakan berbagai software. Maka kesimpulannya adalah: banyak sekali software yang dapat digunakan, antara lain: SPSS, EViews, STATA, Minitab, SPSS AMOS, Excel dan software komputasi lainnya.
Contoh Regresi Linear
Salah satu contoh penelitian yang menggunakan analisis regresi linear adalah penelitian dengan judul: “pengaruh ROA, NPM dan Size Terhadap Return Saham.” Untuk contoh penelitian ini sudah saya jelaskan secara rinci dalam artikel tentang contoh penelitian bisnis dengan regresi linear.
Berdasarkan contoh penelitian diatas, sudah jelas bahwasanya semua variable berskala data interval atau rasio. Dengan kata lain data yang digunakan adalah data kuantitatif atau numeric. Dalam contoh tersebut juga dijelaskan bahwasanya variable bebas atau prediktor adalah lebih dari satu, yaitu ROA, NPM dan Size.
Jika anda ingin melihat contoh data (data fiktif) dan output hasil pengujian regresi linear, dapat anda download di link berikut ini: Download.
Demikian penjelasan saya tentang regresi linear berganda, sedangkan tutorial regresi linear berganda dengan SPSS akan kami bahas dalam artikel selanjutnya.
Baca Juga: Regresi Linear R Studio: Tutorial, Uji Asumsi dan Penjelasan!













terimakasih regresi linear bergandanya
Terima kasih sudah berkunjung
Selamat Pagi mas Anwar,
mohon penjelasannya, apakah regresi linear berganda perlu dilakukan jika varibel terikatnya ” “DUMMY” dan menggunakan varibel moderasi?
Terimakasih
Regresi linear hanya untuk data variabel terikat yang berskala kuantitatif (skala data interval atau rasio)
pagi pak anwar, saya pemula hendak membuat tesis, kalau ada 5 variabel bebas, 2 diantaranya dimoderasi , menggunakan apa pak olah datanya? terimakasih
Anda dapat menggunakan uji regresi linier dengan moderasi atau yang biasa disebut dengan istilah Moderated Regression Analysis (MRA)