Two Way Anova Dengan Excel Tanpa Replikasi
Artikel ini merupakan kelanjutan dari artikel sebelumnya yang berjudul “Two Way Anova dalam Excel“. Pada artikel sebelumnya tersebut, dijelaskan bagaimana caranya melakukan analisa statistik uji Two Way Anova Dengan Replikasi dalam Excel menggunakan Data Analysis Toolpak. Dalam kesempatan ini, kami akan jelaskan tutorial Two Way Anova dengan Excel Tanpa Replikasi.
Agar anda bisa memahami artikel Two Way Anova dengan Excel ini, anda harus mempelajari terlebih dahulu artikel sebelumnya tersebut. Silakan Baca di link berikut: Two Way Anova dalam Excel.
Makna Tanpa Replikasi dalam Two Way Anova dengan Excel
Setelah anda pelajari, maka mari kita simpulkan apa yang dimaksud dengan Two Way Anova dengan Replikasi dalam Excel. Replikasi berarti ada sesuatu yang kembar atau sama. Dalam hal ini, replikasi yang dimaksud adalah adanya beberapa atau lebih dari satu sampel dengan kategori yang sama, baik kategori pertama dan kedua. Ingat bahwa Two Way Anova harus terdiri dari 2 variabel independen yang bersifat kategorik.
Contoh Uji Two Way Anova dengan Excel
Contoh: Penelitian yang meneliti adakah perbedaan pendapatan pada 30 Responden berdasarkan Jenis Kelamin dan Pendidikan. Jenis Kelamin memiliki 2 kategori yaitu pria dan wanita. Pendidikan dengan 3 kategori yaitu SLTP, SLTA dan PT. Ilustrasikan berdasar judul di atas, bahwasanya akan ada 15 orang berjenis kelamin pria dan 15 orang wanita. Masing-masing kelompok pria dan wanita, terdiri dari 3 kelompok pendidikan. Sehingga jika digambarkan dalam bentuk tabel, maka kelompok pria ada 15 orang, dari 15 orang tersebut: 5 orang berpendidikan SLTP, 5 orang SLTA dan 5 orang PT. Kelompok wanita juga ada 15 orang, dari 15 orang tersebut: 5 orang berpendidikan SLTP, 5 orang SLTA dan 5 orang PT.
Untuk lebih jelasnya, lihat tabel di bawah ini:
Dari tabel di atas bisa kita lihat, ternyata masing-masing kelompok kecil terdiri dari 5 sampel. Sehingga dikatakan terdapat 5 replikasi.
Jadi yang dimaksud dengan replikasi di sini adalah banyaknya sampel dengan 2 kategori variabel independen yang sama.
Setelah anda pahami penjelasan di atas, kami berharap anda bisa mengerti sepenuhnya tentang Two Way Anova dengan Replikasi. Selanjutnya kita pahami apa yang dimaksud dengan Two Way Anova Tanpa Replikasi. Silakan lihat tabel di bawah ini:
Dari tabel di atas, bisa kita lihat bahwa tidak ada replikasi. Artinya untuk sampel pria, hanya ada 1 kelompok yang terbagi dalam 3 kelompok kecil, yaitu pria yang SLTP, SLTA dan PT. Begitu juga dengan wanita, hanya satu kelompok seperti pria. Contoh di atas tampaknya tidak sesuai dengan kontek penelitian yang sesungguhnya. Mari kita coba ambil contoh penelitian yang sesuai:
Tutorial Two Way Anova dengan Excel
“Perbedaan Pertumbuhan Bakteri Berdasarkan Temperatur dan Ph“. Kita asumsikan menilai pertumbuhan bakteri dengan menanam bakteri pada media dengan 3 tingkat Ph dan 4 tingkat suhu. Sehingga semua ada 12 botol.
Lihat hasilnya seperti tabel di bawah ini:
Dari data di atas, kita coba lakukan uji Two Way Anova Tanpa Replikasi dengan menggunakan Data Analysis Toolpak di Excel. Apabila aplikasi Excel anda belum diaktifkan, aktifkan terlebih dahulu dengan membaca artikel kami yang berjudul: “Cara Mengaktifkan Analysis Toolpak dalam MS Excel“.
Buat tabel temperatur dan Ph seperti di atas dengan dimulai dari cell A4 s/d D8.
Lihat contoh file excel di bawah ini. Untuk lebih jelasnya anda download file excel di bawah ini pada link berikut:
Two Way Anova Without Replication.xlsx
Caranya adalah:
- Pada menu, klik Data, Data Analysis. maka akan tampak sebagai berikut: Pilih Anova: Two Factor Without Replication. Klik OK. Maka akan tampak jendela di bawah ini:

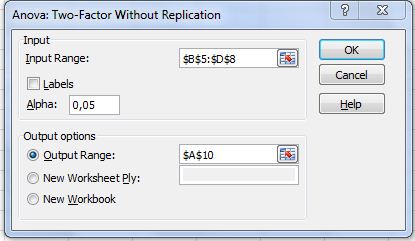
- Pada kotak Input Range arahkan pada cell B5 s/d D8.
- Pada kotak Output Range, arahkan pada cell A10.
- Klik OK.
- Lihat hasilnya dan buat kesimpulan.
Informasi yang diungkapkan oleh analisis di atas: pengaruh suhu tidak berinteraksi dengan efek dari pH. Dengan kata lain, perubahan suhu tidak mengubah respon terhadap pH, dan begitu sebaliknya.Kita dapat menyimpulkan hal ini karena residual (error) mean square (MS) yang kecil dibandingkan dengan MS temperatur (kolom) atau pH (baris). Sebuah mean square residual yang rendah memberitahukan pada kita bahwa sebagian besar variasi dalam data tersebut diperhitungkan dengan efek terpisah dari suhu dan pH.
Kesimpulan Dalam Menjawab Hipotesis Two Way Anova dengan Excel:
- Baris/Row (Ph) P value 0,002 < 0,05 sehingga ada perbedaan pertumbuhan bakteri berdasarkan Ph.
- Kolom/Column (Temperatur) P value 2,870 > 0,05 sehingga tidak ada perbedaan pertumbuhan bakteri berdasarkan temperatur.
- MS Error atau residual kecil dibandingkan MS Row atau MS Column sehingga pengaruh suhu tidak berinteraksi dengan efek dari pH.
Demikian artikel kami tentang uji two way anova dengan excel tanpa replikasi, semoga bermanfaat. Terima Kasih.
By Anwar Hidayat











