KORELASI
Korelasi adalah teknik statistik yang digunakan untuk meguji ada/tidaknya hubungan serta arah hubungan dari dua variabel atau lebih.
Yang akan dibahas dalam pelatihan ini adalah :
1. Korelasi sederhana pearson & spearman
2. Korelasi partial
3. Korelasi ganda.
KOEFISIEN KORELASI
Besar kecilnya hubungan antara dua variabel dinyatakan dalam bilangan yang disebut Koefisien Korelasi:
a. Besarnya Koefisien antara -1 0 +1
b. Besaran koefisien -1 & 1 adalah hubungan yang sempurna
c. Nilai Koefisien 0 atau mendekati 0 dianggap tidak berhubungan antara dua variabel yang diuji
ARAH HUBUNGAN
a. Positif (Koefisien 0 s/d 1)
b. Negatif (Koefisien 0 s/d -1)
c. Nihil (Koefisien 0).
PEARSON CORRELATION
Digunakan untuk data interval & rasio
Distribusi data normal
Terdiri dari dua variabel
1 Variabel X (Independen)
1 Variabel Y (dependen)
CONTOH
Judul: Hubungan antara intensitas belajar dengan prestasi mata kuliah statistik
Variabel X : Intensitas belajar (diukur dari lamanya belajar dalam satu minggu)
Variabel Y : Prestasi matakuliah statistik (diukur dari nilai ujian akhir semester)
Hipotesa:
H0: Tidak ada hubungan antara Intenitas belajar dengan prestasi mata kuliah statistik
Ha: Ada hubungan antara Intenitas belajar dengan prestasi mata kuliah statistik
INPUT DATA KE SPSS
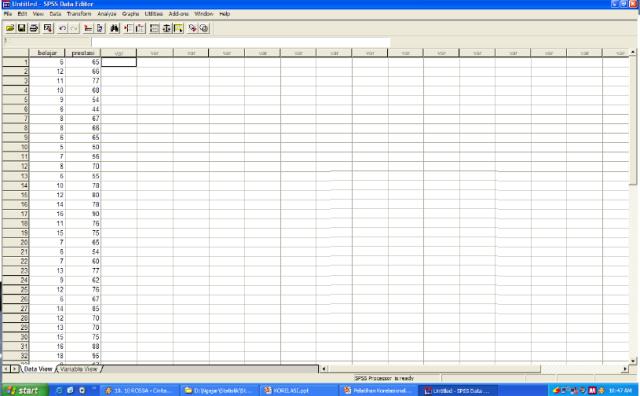
SPSS
Ada dua view dalam SPSS
a. Data View : digunakan untuk memasukkan data yang akan dianalisis
b. Variabel View : digunakan untuk memberi nama variabel dan pemberian koding.
UJI NORMALITAS
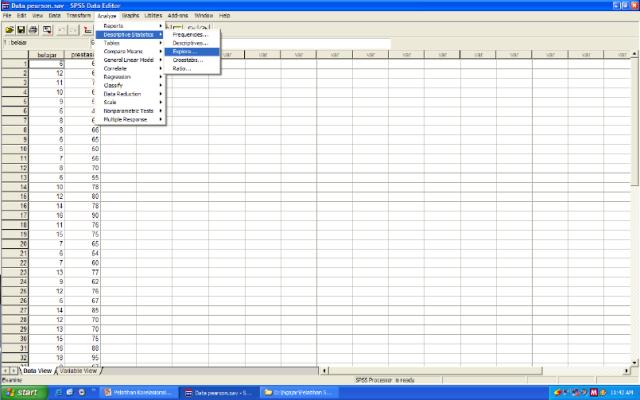

INTERPRESTASI NORMALITAS
TAHAP ANALISIS
INTERPRESTASI
Untuk pengambilan keputusan statistik, dapat digunakan 2 cara:
1. Koefisien Korelasi dibandingkan dengan nilai r tabel (korelasi tabel)
Apabila Koefisien Korelasi > r tabel, Maka ada hubungan yang signifikan (Ha Diterima),
Apabila Koefisien Korelasi < r tabel, Maka tidak ada hubungan yang signifikan (H0 Diterima).
2. Melihat Sig.
Apabila nilai Sig. < 0,05 Maka ada hubungan yang signifikan (Ha Diterima)
Apabila nilai Sig. > 0,05 Maka tidak ada hubungan yang signifikan (H0 Diterima)
Arah hubungan:
Dilihat dari tanda koefisien:
Tanda (-) berarti apabila variabel X tinggi maka variabel Y rendah
Tanda (+) berarti apabila variabel X tinggi maka variabel Y juga tinggi
SPEARMAN
a. Digunakan untuk jenis data ordinal
b. Cara analisis dan interpretasi sama dengan Pearson.
c. Perbedaan hanya pada waktu memilih box yang diaktifkan adalah box spearman.
KORELASI PARTIAL
Korelasi yang digunakan untuk menguji hubungan dua atau lebih variabel independen dengan satu variabel dependen dan dilakukan pengendalian pada salah satu variabel independennya
CONTOH
Judul: Hubungan antara biaya promosi dan penjualan dengan mengendalikan jumlah outlet
Variabel X1: Biaya Promosi
Variabel X2: Jumlah outlet (dikendalikan)
Variabel Y: Penjualan
Hipotesa:
H0: Tidak ada hubungan antara biaya promosi dengan penjualan apabila jumlah outlet dikendalikan
Ha: Ada hubungan antara biaya promosi dengan penjualan apabila jumlah outlet dikendalikan
CONTOH
Buka data : Korelasi ganda dan partial.sav Data
ANALISIS
KORELASI PARTIAL
OUTPUT PARTIAL
KORELASI GANDA
Koefisien yang digunakan untuk menguji hubungan dua atau lebih variabel independen dengan satu variabel dependen secara bersamaan.
CONTOH
Judul: Hubungan antara biaya promosi dan jumlah outlet dengan penjualan
Variabel X1: Biaya Promosi
Variabel X2: Jumlah outlet
Variabel Y: Penjualan
Hipotesa:
H0: Tidak ada hubungan antara biaya promosi dan jumlah outlet dengan penjualan
Ha: Ada hubungan antara biaya promosi dan jumlah outlet dengan penjualan
CONTOH
Buka data : Korelasi ganda dan partial.sav Data
KORELASI GANDA
INTERPRESTASI KORELASI GANDA
a. Untuk menginterprestasi korelatif ganda lihat nilai R, semakin mendekati 1 maka hubungan semakin kuat
b. Guna memperkaya analisis, sebelum dianalisis korelasi ganda dapat juga ditambahkan analisis korelasi pada masing-masing variabel independen dengan variabel dependen (caranya sama dengan analisis korelasi pearson).
REGRESI
a. Analisis regresi adalah analisis lanjutan dari korelasi
b. Menguji sejauh mana pengaruh variabel independen terhadap variabel dependen setelah diketahui ada hubungan antara variabel tersebut
c. Data harus interval/rasio
d. Data Berdistribusi normal.
Yang akan dibahas dalam pelatihan ini adalah:
a. Regresi sederhana: yaitu regresi untuk 1 variabel independen dengan 1 variabel dependen
b. Regresi ganda: yaitu regresi untuk lebih dari satu variabel independen dengan 1 variabel dependen.
REGRESI SEDERHANA
Buka data : Pearson.sav Data
INTERPRETASI REGRESI SEDERHANA
Output 1
Lihat nilai R = 0,843 ini berarti bahwa kekuatan hubungan antara variabel X dengan Y adalah 0,843
INTERPRETASI REGRESI SEDERHANA
OTPUT 2
- Untuk melihat signifikansi persamaan regresi dapat dilihat dari nilai F = 81,329 dan dibandingkan dengan F tabel
- Apabila nilai F < F tabelmaka persamaan garis regresi tidak dapat digunakan untuk prediksi
- Apabila nilai F > F tabelmaka persamaan garis regresi dapat digunakan untuk prediksi
- Selain itu dapat pula dengan melihat nilai Sig. dapat digunakan untuk prediksi apabila nilai Sig. < 0,05
INTERPRETASI REGRESI SEDERHANA
OUTPUT 3
- Untuk membuat persamaan garis regresi dapat dilihat dari kolom B.
- Constan = 38,481 dan intensitas belajar= 2,978
- Berarti persamaan garisnya adalah: Y=38,481 + 2,978 X.
REGRESI BERGANDA
- Digunakan untuk analisis regresi dengan jumlah variabel independen lebih dari satu dengan satu variabel dependen
- Ada tambahan asumsi yang harus dipenuhi, yaitu tidak boleh ada hubungan antar variabel-variabel independennya (uji multikolinearitas).
CONTOH
Buka data : Korelasi ganda dan partial.sav
INTERPRETASI REGRESI GANDA
Output 1
Lihat nilai R = 0,976 ini berarti bahwa kekuatan hubungan antara variabel X1dan X2 secara bersamaan dengan Y adalah 0,976.
INTERPRETASI REGRESI GANDA
Output 2
Untuk melihat signifikansi persamaan regresi dapat dilihat dari nilai F = 118,294 dan dibandingkan dengan Tabel F: F Tabel dalam Excel
- Apabila nilai F < F tabelmaka persamaan garis regresi tidak dapat digunakan untuk prediksi
- Apabila nilai F > F tabelmaka persamaan garis regresi dapat digunakan untuk prediksi
- Selain itu dapat pula dengan melihat nilai Sig. dapat digunakan untuk prediksi apabila nilai Sig. < 0,05
INTERPRETASI REGRESI GANDA
Output 3
Untuk membuat persamaan garis regresi dapat dilihat dari kolom B.
- Constan = 64,639
- Biaya promosi= 2,342
- Jumlah Outlet= 0,535
- Berarti persamaan garisnya adalah: Y=64,639 + 2,342 biaya promosi + 0,535 Jumlah Outlet
INTERPRETASI REGRESI GANDA
Output 4
Identifikasi kolinieritas dapat dilakukan dengan melihat:
- Output 3, Kolom VIF. : terjadi kolinearitas apabila nilai VIF > 5
- Output 4, Kolom eugenvalue: terjadi kolinearitas apabila nilai eugenvalue mendekati 0
- Output 4, Kolom condition index: terjadi kolinearitas apabila nilai condition index > 15. Dikatakan parah apabila > 30.
Pelajari tentang: Regresi Linear Berganda.
By Anwar Hidayat







































sangat membantu, trims
Trims!
Untuk membuktikan hasil uji korelasi apakah bermakna atau dapat mewakili keseluruhan populasi.
Tnya dong…
kenapa nilai r korelasi harus dibandingkan dengan nilai r tabel
Tergantung pada skala data tiap variabel. Anda telusuri pada artikel saya di blog ini tentang regresi linear, regresi logistik, anova, ancova, manova, mancova, dll.
saya mau tanya.apabila judul skripsi saya hubungan antara kedalaman laut dan panjang jaring terhadap jumlah hasil tangkapan udang.sebaiknya saya menggunakan uji statistik apa?terima kasih
H1 diterima atau ada hubungan yang bermakna apabila r hitung > r tabel.
Kemudian Ha dan H0 nya apa ya untuk uji hipotesisnya yang bisa menyimpulkan Ha di terima atau di tolak
Gunakan Uji Koefisien Phi atau Cramer
Mau tanya pak skripsi saya mencari hubungan antar 2 varibel, untuk kedua variabel menggunakan dikotomi semua dengan skor pernyataan ya =1, tidak = 0. Untuk analisis dapat menggunakan uji statistik apa? Trims
Makasih mas, atas share nya, kebetulan saya baru mau mendalami tentang ststistik…
Sangat membantu mas… 🙂
Tidak bisa, syarat uji pearson adalah skala data interval atau rasio. Sebaiknya anda menggunakan uji spearman, kendall tau, gamma atau somer's. Baca artikel saya tentang hal itu.
pak saya mau tnya, skripsi saya mencari hubungan antara dua variabel dan kedua variabel tersebut menggunakan skala ordinal, apa bisa analisis datanya menggunakan uji pearson?
maksih..sangat membantu
Jika bentuk hipotesisnya adalah asosiatif, maka gunakan analisis untuk derajat yang terendah. Bila Nominal Vs Ordinal, maka gunakan analisis asositaif untuk data nominal, misalnya uji koefisien kontingensi.
analisis data apa yang digunakan apabila variabel independennya nominal dan variabel dependennya ordinal..
Mantaap
Sangat membantu
Terimakasih banyak
Sama-sama, harap share ya
pak mau tanya, kalo datanya ordinal vs interval lebih baik pake uji apa ya?
Jika bentuk hipotesis anda adalah korelasi, maka gunakan uji korelasi untuk variabel dengan derajat yang lebih rendah. Jika interval dengan ordinal, maka gunakan uji korelasi untuk ordinal, misalnya uji kendall tau.
Assalamualaikum wr.wb. Terima kasih buat admin, bermanfaat sekali teori korelasi statistika ini. Semoga diberkahi oleh Allah SWT dalam berbagi ilmu yg bermanfaat. Aamiin
Terima kasih juga, selamat telah berkunjung ke website kami
Assalamualaikum, terima kasih atas postingannya, krn sngat membantu,sy mau nanya bagaimna cara menganlisis data corelasi menggunakan spss dengan 1 variabel independent dan 1 variable dependen.
Silahkan baca artikel kami: regresi linear sederhana dengan SPSS.
Bagaimana jika nilai signifikan nya 0,052 > 0,05
Atau nilai signifikannya sama 0,05=0,05
Apakah ada hububgan yang signifikan atau tidak ada hubungan??
Karena 0,052 > 0,05 maka terima H0 atau tidak ada hubungan yang signifikan.
Saya meneliti pengaruh suku bunga terhadap uang beredar m1.
Hasilnya uji t nya menunjukkan 0,052>0,05. Dengan kata lain, tidak ada pengaruh.
Tetapi menurut para ahli mengatakan, suku bunga berpengaruh negatif terhadap uang beredar m1.
Tapi hasilnya menunjukkan tidak ada pengaruh, itu kenapa bisa tidak berpengaruh pak??
Secara statistik berarti memang tidak ada pengaruh signifikan dari hasil penelitian anda. Mengapa berbeda dengan konsep yang ada, maka anda sendiri harusnya yang lebih tahu hal tersebut. Mungkinkah ada kesalahan olah data atau prosedur pengumpulan data. Ataukah memang ada anomali pada sampel yang anda gunakan. Ataukah memanga ada faktor penting lainnya yang berpengaruh.
Kalau data ordinal bagaimana cara menguji regresi berganda
Baca regresi ordinal.
Halo, saya mau tanya bila nilai r atau korelasi yang didapat itu kecil/rendah faktor apa sih yang menyebabkan hal tersebut ? dan faktor apa yang dapat meningkatkan nilai korelasi/ r menjadi lebih baik? terima kasih 🙂
Nilai r korelasi itu tinggi atau rendah kembali lagi kepada hubungan kedua data tersebut. Jika memang terdapat keeratan hubungan maka otomatis nilai r korelasi nya tinggi, begitu pula sebaliknya. Namun memang ada beberapa hal yang bisa menyebabkan nilai r itu sedikit melenceng dari yang seharusnya, misalnya adanya data pencilan atau outlier serta distribusi data yang tidak normal.
Pak Anwar spearman dan Kendall tau kan sama-sama uji korelasi untuk skala ordinal. Apa perbedaannya pak? Karena saya bingung memilih antara spearman dan kendall. Terima kasih pak
Pada dasarnya sama saja fungsi kedua uji tersebut. Hanya saja, spearman rho sebaiknya digunakan untuk uji korelasi data ordinal yang sumber datanya dari 2 subjek yang berbeda. Misalnya 2 orang guru melakukan penilaian terhadap sikap siswa. Kemudian penilaian kedua guru tersebut dinilai apakah terdapat kesesuaian. Jika sesuai dapat diartikan terdapat korelasi penilaian dari kedua guru tersebut. Sedangkan Kendall tau digunakan untuk uji korelasi dat la ordinal yang sumber datanya dari 1 subjek. Misalnya uji korelasi IQ siswa dengan nilai ujian matematika. Disini sebagai subjek adalah siswa, dimana setiap 1 siswa mempunyai 2 data yaitu data IQ dan data nilai ujian matematika.
ka mau tanya klo uji korelasi ada di eviews ga ya ka?
Ada