Pengertian Analisis Regresi Korelasi Dan Cara Hitung
Analisis Regresi Linear
Analisis regresi mempelajari bentuk hubungan antara satu atau lebih peubah/variabel bebas (X) dengan satu peubah tak bebas (Y). Dalam penelitian peubah bebas ( X) biasanya peubah yang ditentukan oleh peneliti secara bebas misalnya dosis obat, lama penyimpanan, kadar zat pengawet, umur ternak dan sebagainya.
Disamping itu peubah bebas bisa juga berupa peubah tak bebasnya, misalnya dalam pengukuran panjang badan dan berat badan sapi, karena panjang badan lebih mudah diukur maka panjang badan dimasukkan kedalam peubah bebas (X), sedangkan berat badan dimasukkan peubah tak bebas (Y).
Sedangkan peubah tak bebas (Y) dalam penelitian berupa respon yang diukur akibat perlakuan/peubah bebas (X). misalnya jumlah sel darah merah akibat pengobatan dengan dosis tertentu, jumlah mikroba daging setelah disimpan beberapa hari, berat ayam pada umur tertentu dan sebagainya.
Tujuan Regresi Linear
Regresi linier adalah salah satu dari jenis analisis peramalan atau prediksi yang sering digunakan pada data berskala kuantitatif (interval atau rasio).
Tujuan dilakukannya regresi linear antara lain adalah:
Apakah seperangkat atau sekumpulan variabel prediktor signifikan dalam memprediksi variabel respon?
Variabel predictor manakah yang signifikan dalam menjelaskan variable respon? Hal ini ditunjukkan dengan koefisien estimasi regresi. Koefisien estimasi inilah yang nantinya akan membentuk persamaan regresi.
Untuk mempelajari cara melakukan analisis regresi linear, silahkan baca artikel kami antara lain:
Regresi Linear Sederhana dengan SPSS
Regresi Linear Berganda dengan Minitab
Regresi Linear Berganda dengan STATA
Analisis Regresi dalam Excel
Bentuk Hubungan Variabel Bebas dan Terikat
Bentuk hubungan antara peubah bebas (X) dengan peubah tak bebas (Y) bisa dalam bentuk polinom derajat satu (linear) polinom derajat dua (kuadratik). Polinom derajat tiga (Kubik) dan seterusnya. Disamping itu bisa juga dalam bentuk lain misalnya eksponensial, logaritma, sigmoid dan sebagainya. Bentuk-bentuk ini dalam analisis regresi-korelasi biasanya dilakukan transformasi supaya menjadi bentuk polinom.
Persamaan Regresi
Dalam bentuk yang paling sederhana yaitu satu peubah bebas (X) dengan satu peubah tak bebas (Y) mempunyai persamaan:
Y =a +bx
Disini a disebut intersep dan b adalah koefisien arah atau koefisien beta.
Dalam pengertian fungsi persamaan garis Y + a + bx hanya ada satu yang dapat dibentuk dari dua buah titik dengan koordinat yang berbeda yaitu ( X1, Y1) dan X2,Y2). Hal ini berarti kita bisa membuat banyak sekali persamaan garis dalam bentuk lain melalui dua buat titik yang berbeda koordinatnya/tidak berimpit.
Persamaan garis melalui dua buah titik dirumuskan sebagai berikut:
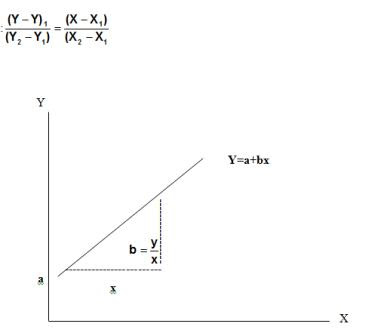
Contoh Persamaan Regresi
Sebagai contoh misalnya titik A (1,3) dan titik B ($,9) maka persamaan garis linear yang dapat dibuat adalah:
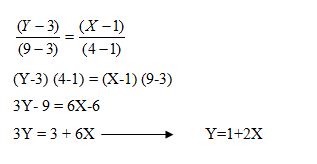
Dalam bentuk matrik bisa kita buat persaman sebagai berikut:

Jadi a=1 dan b=2 sehingga persamaannya Y=1 +2X
Jika jumlah data sebanyak n maka persamaannya sebagai berikut:
Disini βo adalah penduga a, β1 adlah penduga b dan εi merupakan besarnya simpangan persamaan garis penduga. Semakin kecil nilai εi persamaan regresi yang diperoleh akan semakin baik.
Penulisan pengamatan
Jadi kita dapat menuliskan pengamatan kita menjadi:
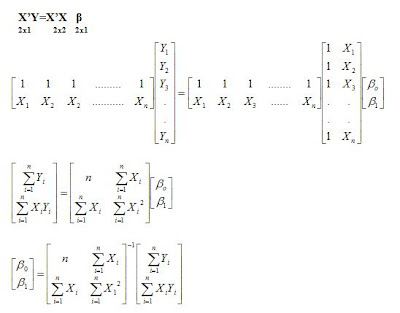
Dengan notasi matriks dapat ditulis sebagai berikut:
Jadi kita peroleh matrik Y,X,β dan ε dengan dimensi sebagai berikut :
Jika diasumsikan E(ε) = 0 maka E(Y) = Xβ
Bila modelnya benar β merupakan penduga terbaik yaitu dengan jalan melakukan penggandaan awal dengan X’ sehingga diperoleh persamaan normal sebagai berikut:
Jadi β=(X’X)-1X’Y
Disini(X’X)-1 adalah kebalikan (inverse) dari matrik X’X
Contoh Perhitungan Regresi
Seorang peneliti ingin mengetahui bentuk hubungan antara jumlah cacing jenis tertentu dengan jumlah telurnya pada usus ayam buras. Untuk tujuan tersebut diperiksa 20 ekor ayam dan ditemukan sebagai berikut:
Tabel 1 jumlah cacing dan jumlah telurnya pada usus ayam buras.
Dari data diatas kita bisa menghitung:
Bila kita duga bentuk hubungan antara jumlah cacing (X) dan jumlah telurnya (Y) adalah:
Jadi Ŷ=-2,442 + 4,103 Xi,
Persamaan Garis regresi Banyak Jenisnya
Persamaan garis regresi Yi =-2,442 + 4,103 Xi bukanlah satu-satunya garis penduga untuk menyatakan hubungan antara jumlah cacing dengan jumlah telurnya. Sudah barang tentu masih banyak lagi bentuk persamaan penduga yang dapat dibuat misalnya dalam bentuk persamaan Yi=βo+β1Xi+β2Xi2,Yi=βoXiβ1(dalam bentuk linear LnYi=Ln βo+βiLnXi) dan masih banyak lagi bentuk yang lainnya.
Untuk menyatakan apakah garis yang diperoleh cukup baik untuk menggambarkan hubungan antara peubah bebas (X) dengan peubah tak bebas (Y) dapat dilakukan pengujian bentuk model yang digunakan dan keeratan hubungannya (korelasi) untuk menyatakan ketepatan dan ketelitian persamaan garis regresi yang diperoleh.
Demikianlah penjelsan singkat kami tentang Analisis Regresi Linear. Agar anda memahami artikel ini, pelajari juga tentang Uji F dan Uji T: “Uji F dan Uji T“
Pelajari juga: Interprestasi Regresi Linear Berganda dengan Minitab dan regresi linear berganda.
By Anwar Hidayat









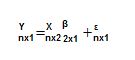

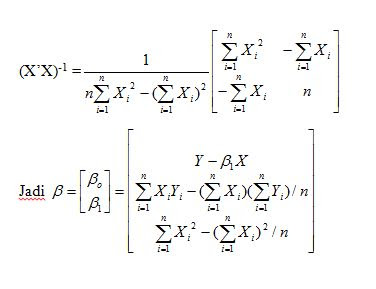

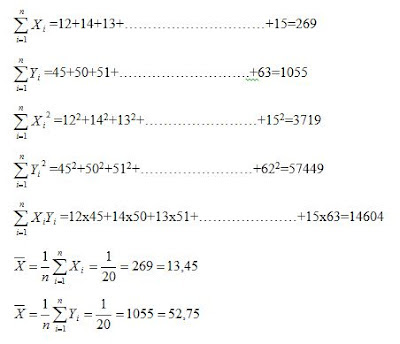

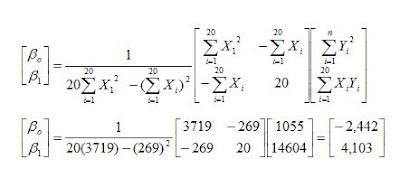







Lihat dari nilai Koefisien Korelasinya, misal uji pearson: apabila nilai r: > 0 sd 0,2 (lemah), 0,2 sd 0,4 (agak lemah), 0,4 sd 0,6 (sedang), 0,6 sd 0,8 (agak kuat), 0,8 sd <1 (kuat), 0 (tidak ada hubungan), 1 (sempurna). Nilai negatif sama dengan positif hanya beda arah hubungan.
Numpang nanya mas kalo nentuin hubungan korelasi kuat ato tidak kuatnya dr mana yah? Terima ksh
Tidak apa-apa dan gunakan untuk pengujian hipotesa dengan mengubah model regresi anda sesuai transformasinya, misal: Y = Beta Constanta + Beta (Sqrt(Var Asli X1 + 1)) + Beta (Var Asli X2)
Tidak apa-apa dan gunakan untuk pengujian hipotesa dengan mengubah model regresi anda sesuai transformasinya, misal: Y = Beta Constanta + Beta (Sqrt(Var Asli X1 + 1)) + Beta (Var Asli X2)
maaf mas kalau beda topik dikit he2..
ane pada uji asumsi klasik menggunakan transformasi sqrt(var. asli + 1) soalnya datanya banyak yang min apakah itu gak pa2??
trus apakah transformasi tersebut juga digunakan ke analisis regresi linier berganda (pengujian hipotesis)??..
makasih..
Regresi itu pada variabelnya, bukan pada itemnya.
Aslm.. mas boleh nanya g?? regresi linier yg mana dipakai kalo instrumen penelitianx memakai 2 kuesioner skala Likert dgn masing-masing kuesioner 20 items pertanyaan.. 10 positif n 10 negatif..
korespondenx skitar 100 org..
Uji korelasi itu hubungan, sedangkan uji F itu uji beda berdasarkan varians. Sedangkan uji t itu uji beda berdasarkan Mean. Untuk menguji keterkaitan 2 variabel, maka digunakan uji korelasi, misalkan uji pearson product moment, uji spearman dan kendall tau, somer's d, gamma, koefisien kontingensi, phi dan cramer.
r itu koefisien korelasi
maaf, mau tanya. perbedaan uji korelasi dengan uji F atau T itu apa ya? untuk mengetahui keterkaitan antara 2 macam variabel sebaiknya memakai uji yang mana? terima kasih.
mohon mav, saya benar2 belajar. nilai r it apa y? lalu bagaimana cara mencari nilai r?
Kalau Uji Korelasi itu untuk menilai kekuatan hubungan antara 2 variabel. Sedangkan regresi adalah untuk meramalkan atau memprediksi nilai variabel terikat berdasarkan nilai variabel bebas. Jadi tujuannya yang berbeda.
kak mau tanya kalau judulnya pengaruh-terhadap dengan 1 variabel bebas dan 1 variabel terikat , lebih cocok pakai korelasi atau regresi? atau menggunakan keduanya? terima kasih.
assalamualaikum
mau ty mas, kalau mau menggunakan regresi linear berganda setelah uji validitas dan reliabilitas apa diharuskan melakukan uji asumsi klasik atau tidak juga ga pa2. kira2 ada pengaruh nya ga sama hasil penelitian dan hipotesis jika kita melakukan uji asumsi klasik dengan tidak melakukan uji asumsi klasik dulu.
wasalam.
Nb.ditunggu informasinya, terimakasih
Perlu dipahami bahwa uji validitas reliabilitas tidak ada hubungan atau kaitannya secara langsung dengan asumsi klasik. Uji validitas reliabilitas itu terkait dengan instrumen untuk pengambilan data apakah telah sahih dan handal. Sedangkan asumsi klasik adalah kriteria yang harus dipenuhi dalam pengujian parametris agar tidak terjadi bias, yaitu pada perhitungan yang sifatnya rentan terhadap pelanggaran asumsi, misalnya estimator ordinary least square (OLS) pada regresi linier. Kalau kita bicara regresi linier, maka uji asumsi seharusnya dilakukan setelah uji regresi linier. Mengapa demikian, karena uji asumsi regresi linier itu menggunakan nilai-nilai residual hasil persamaan regresi linier. Jadi otomatis lakukan dulu uji regresi linier maka baru mendapatkan nilai y prediksi. Selanjutnya dari nilai y prediksi bisa kita hitung nilai-nilai residual. Selanjutnya dapat dilakukan uji asumsi berdasarkan nilai residual tersebut. Misalnya asumsi normalitas yang mengukur distribusi residual. Uji autokorelasi yang mengukur serial korelasi dari residual. Uji heteroskedastisitas yang mengukur korelasi antara residual dengan y prediksi. Deteksi outlier yang menilai adanya data pencilan pada residual. Dan uji multikolinearitas yang menilai interkorelasi dan kovarians sisaan variabel oleh residual.
ka izin bertanya, analisis apa yang cocok saya gunakan apabila saya ingin mengetahui pengaruh dari variabel X terhadap variabel Y. tetapi pada variabel X data tidak terdistribusi normal dan data diambil dari sampel jenuh (populasi=sampel)?
mohon bantuannya ka.
Jika yang dimaksud adalah uji regresi linear, maka asumsi normalitas adalah pada residualnya bukan pada masing-masing variabel bebas atau terikatnya. SIlahkan baca artikel kami: regresi linear berganda.