Uji Binomial
Pengertian Uji Binomial
Uji binomial adalah uji non parametric yang digunakan untuk menggantikan uji statistik t jika asumsi n kecil dan populasi normal sebagai syarat uji t tidak dipenuhi.
Hipotesis Uji Binomial
Dengan uji Hipotesis sebagai berikut:

Karena uji binomial adalah salah satu uji komparatif atau uji beda, maka cara menjawab hipotesis di atas adalah:
- Ho diterima artinya tidak terdapat perbedaan bermakna.
- H1 diterima artinya terdapat perbedaan bermakna.
Cara Menjawab Hipotesis
Statistik Uji: Melihat nilai sig atau p-value yang diperoleh pada software pendukung (misal SPSS).
Daerah Kritis:
Ho ditolak jika p-value atau sig < Alfa
Dalam perangkat SPSS, kita dapat melakukan Binomial Test dengan cara:
Klik Analyze -> Nonparametric Test -> Binomial
(keterangan lebih lanjut akan dipaparkan dalam contoh soal).
Contoh Soal Uji Binomial
Berdasarkan penjelasan di atas, kita coba membuatkan sebuah studi kasus atau contoh uji yang dibahas dalam tutorial ini. Yaitu:
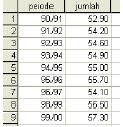
Akan diuji apakah rata-rata jumlah sekolah menengah pertama negeri setiap tahunnya yang mendapatkan bantuan sama dengan 50 persen sekolah dari total seluruh sekolah (dalam persen), untuk itu diambil data beberapa periode yang disajikan ke dalam tabel di bawah ini:

Uji Binomial dengan SPSS
Cara Penyelesaian Menggunakan SPSS:
1. Inputkan data ke dalam SPSS
2. Klik Analyze -> Nonparametric Test -> Binomial
Muncul kotak dialog berikut:

- Pada test variable list masukan Jumlah
- Pada Define Dichotomy aktifkan Cut Point dan ketikkan nilai yang akan diuji dalam hal ini 50
- Klik OK.
3. Outputnya adalah:
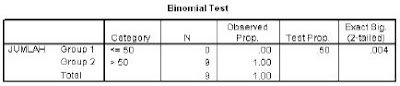
Dari output diperoleh bahwa banyaknya data yang lebih dari 50 = 9 dengan proporsi 1,0 dan tidak ada data yang kurang dari 50.
Maka selanjutnya akan dilakukan uji hipotesis:

Tingkat signifikansi Alfa = 5 %.
Statistik Uji diperoleh nilai sig = 0,004.
Daerah Kritis: Ho ditolak jika sig < Alfa = 0,05.
Kesimpulan:
Oleh karena nilai sig = 0,004 < Alfa = 0,05 maka Ho ditolak yang berarti bahwa rata-rata sekolah yang menerima bantuan setiap tahunnya tidak sama dengan 50 persen dari total semua SMP.
By Anwar Hidayat










