Pengertian Multikolinearitas dan Dampaknya

Multikolinearitas

Definisi Multikolinearitas

Multikolinearitas adalah sebuah situasi yang menunjukkan adanya korelasi atau hubungan kuat antara dua variabel bebas atau lebih dalam sebuah model regresi berganda. Model regresi yang dimaksud dalam hal ini antara lain: regresi linear, regresi logistik, regresi data panel dan cox regression.

Gejala Multikolinearitas

Dalam situasi terjadi multikolinearitas dalam sebuah model regresi berganda, maka nilai koefisien beta dari sebuah variabel bebas atau variabel predictor dapat berubah secara dramatis apabila ada penambahan atau pengurangan variabel bebas di dalam model. Oleh karena itu, multikolinearitas tidak mengurangi kekuatan prediksi secara simultan, namun mempengaruhi nilai prediksi dari sebuah variabel bebas. Nilai prediksi sebuah variabel bebas disini adalah koefisien beta. Oleh karena itu, sering kali kita bisa mendeteksi adanya multikolinearitas dengan adanya nilai standar error yang besar dari sebuah variabel bebas dalam model regresi.

Berdasarkan penjelasan di atas, maka dapat disimpulkan bahwa, jika terjadi multikolinearitas, maka sebuah variabel yang berkorelasi kuat dengan variabel lainnya di dalam model, kekuatan prediksinya tidak handal dan tidak stabil. Dan pengertian multikolinearitas adalah sesungguhnya terletak pada ada atau tidak adanya korelasi antar variabel bebas.

Penyebab Multikolinearitas

Penyebab multikolinearitas adalah adanya korelasi atau hubungan yang kuat antara dua variabel bebas atau lebih, seperti yang sudah dijelaskan di atas. Namun penyebab lainnya yang dapat menyebabkan hal tersebut secara tidak langsung adalah, antara lain:

1. Penggunaan variabel dummy yang tidak akurat di dalam model regresi. Akan lebih beresiko terjadi multikolinearitas jika ada lebih dari 1 variabel dummy di dalam model.
2. Adanya perhitungan sebuah variabel bebas yang didasarkan pada variabel bebas lainnya di dalam model. Hal ini bisa dicontohkan sebagai berikut: dalam model regresi anda, ada variabel X1, X2 dan Perkalian antara X1 dan X2 (X1*X2). Dalam situasi tersebut bisa dipastikan, terdapat kolinearitas antara X1 dan X1*X2 serta kolinearitas antara X2 dengan X1*X2.
3. Adanya pengulangan variabel bebas di dalam model, misalkan: Y = Alpha + Beta1 X1 + Beta2 X1*5 + Beta3 X3 + e.

Dampak dari Multikolinearitas

Dampak

Dampak dari multikolinearitas antara lain:

1. Koefisien Partial Regresi tidak terukur secara presisi. Oleh karena itu nilai standar errornya besar.
2. Perubahan kecil pada data dari sampel ke sampel akan menyebabkan perubahan drastis pada nilai koefisien regresi partial.
3. Perubahan pada satu variabel dapat menyebabkan perubahan besar pada nilai koefisien regresi parsial variabel lainnya.
4. Nilai Confidence Interval sangat lebar, sehingga akan menjadi sangat sulit untuk menolak hipotesis nol pada sebuah penelitian jika dalam penelitian tersebut terdapat multikolinearitas.

Contoh

Untuk memudahkan para pembaca memahami dampak di atas, kami coba ilustrasikan sebagai berikut:

Anda harus pahami dulu yang dimaksud dengan koefisien regresi parsial. Dalam hal ini biasanya lebih dikenal dengan istilah koefisien Beta. Koefisien Beta itu seperti yang ada dalam contoh persamaan regresi berikut: Y = Alpha + Beta1 X1 + Beta2 X2 + e.

Contoh Model Regresi dengan Masalah Multikolinearitas

Berikut kami contohkan sebuah model regresi yang terdapat masalah multikolinearitas, yaitu dengan persamaan Y = Alpha + Beta1 X1 + Beta2 X2 + Beta3 X1*X2 + e. (Dimana X1*X2 adalah hasil perkalian antara X1 dengan X2).

Apabila kita punya data sebagai gambar berikut: ada X1, X2 dan Perkalian antara X1 dengan X2 yaitu X1X2.

Pertama kali kita lakukan regresi tanpa melibatkan variabel X1X2, yaitu: persamaan Y = Alpha + Beta1 X1 + Beta2 X2 + Beta3 X1*X2 + e. Berikut Hasilnya:

Deteksi Multikolinear dengan Nilai Standar Error

Perhatikan di atas: Nilai Standar Error X2 sebesar 1,044 dimana nilainya > 1. dan nilai standar error Constant 3,887 dimana juga nilainya > 1. Hal ini menunjukkan bahwa dengan adanya multikolinearitas, nilai standar error menjadi besar, sehingga nilai Koefisien Beta (B) tidak dapat mengukur variabel terikat secara presisi.

Deteksi Multikolinear dengan Nilai Confidence Interval

Perhatikan nilai Confidence Interval, baik Lower Bound maupun Upper Bound, rentangnya sangat lebar. Misal pada X1, rentangnya antara -0,827 sd 3,108. Dan pada X2 nilai rentangnya -1,138 sd 3,066. Hal ini yang menyebabkan nilai signifikansi t parsial di atas lebih dari batas kritis 0,05 atau terima H0, yaitu pada X1 sebesar 0,249, pada X2 sebesar 0,361 dan pada X1*X2 sebesar 0,595. Hal ini menunjukkan bahwa, keberadaan sebuah variabel yang berkorelasi kuat dengan variabel lainnya di dalam model dapat menyebabkan perubahan secara dramatis nilai koefisien regresi parsial. Berikut akan kami buktikan sebagai berikut:

Contoh Output Tanpa Multikolinearitas

Kita akan bandingkan apabila model regresi tanpa melibatkan variabel X1*X2, hasilnya adalah di bawah ini:

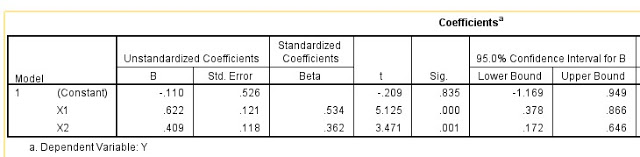
Lihat pada tabel “Output Non Multikolinear”, jika tanpa variabel penyebab multikolinearitas yaitu X1*X2, maka hasilnya: Nilai standar error pada X1, X2 dan constant adalah kurang dari 1. Nilai Rentang Confidence Interval sempit, yaitu pada X1 rentangnya 0,378 sd 0,866 dan pada X2 rentangnya 0,172 sd 0,646, sehingga signifikansi t parsial adalah pada X1 sebesar 0,000 dan pada X2 sebesar 0,001 dimana keduanya kurang dari batas kritis 0,05 atau dapat diartikan keduanya terima H1. Hasil diatas menunjukkan bahwa sesungguhnya X1 dan X2 linear terhadap variabel terikat, namun dengan penambahan variabel yang menyebabkan multikolinearitas, maka nilai signifikansi t parsial berubah secara drastis. Sehingga dapat diambil kesimpulan bahwa sesungguhnya nilai prediksi yang dihasilkan pada model yang terdapat multikolinearitas (tabel Output Multicollinearity) tidak dapat memprediksi variabel terikat secara presisi.

Cara mendeteksi Multikolinearitas

Cara mendeteksi adanya Multikolinearitas di dalam model regresi adalah dengan cara:

1. Melihat kekuatan korelasi antar variabel bebas. Jika ada korelasi antar variabel bebas > 0,8 dapat diindikasikan adanya multikolinearitas.
2. Melihat nilai standar error koefisien regresi parsial. Jika ada nilai standar error > 1, maka dapat diindikasikan adanya multikolinearitas.
3. Melihat rentang confidence interval. Jika rentang confidence interval sangat lebar, maka dapat diindikasikan adanya multikolinearitas.
4. Melihat nilai Condition Index dan eigenvalue. Jika nilai condition index > 30 dan nilai eigenvalue < 0,001 dapat diindikasikan adanya multikolinearitas.
5. Melihat nilai Tolerance dan Variance Inflating Factor (VIF). Jika nilai Tolerance < 0,1 dan VIF > 10 dapat diindikasikan adanya multikolinearitas. Sebagian pakar menggunakan batasan Tolerance < 0,2 dan VIF > 5 dalam menentukan adanya multikolinearitas. Para pakar juga lebih banyak menggunakan nilai Tolerance dan VIF dalam menentukan adanya Multikolinearitas di dalam model regresi linear berganda dibandingkan menggunakan parameter-parameter yang lainnya. Hal ini juga dalam prakteknya menggunakan SPSS, kita sudah disuguhkan dengan hasil yang instant, dimana kita bisa langsung lihat nilai keduanya di dalam output SPSS.

Kapan Bisa Dipertahankan

Ada kalanya kita tetap mempertahankan adanya multikolinearitas di dalam model regresi. Yaitu jika kita berada dalam kondisi sebagai berikut:

Nilai VIF tinggi hanya pada variabel kontrol, sedangkan pada variabel interest, nilai VIF rendah.

Meskipun pada variabel kontrol nilai VIF tinggi, tetapi pada variabel interest nilai VIF rendah, maka dapat diartikan bahwa nilai prediksi dari variabel yang menjadi bahan perhatian dalam model tetap dapat mengukur variabel terikat secara presisi. Mengapa bisa seperti itu? kami akan ilustrasikan, misalkan model kita ada 3 variabel, yang menjadi variabel interest adalah variabel dummy, yaitu Jenis Kelamin (Laki-laki dan perempuan). Sedangkan variabel kontrol ada 2, yaitu penghasilan bulanan dan belanja bulanan. Dalam hal ini, antara kedua variabel kontrol terdapat korelasi yang kuat, sehingga VIF keduanya tinggi. Namun keduanya tidak berkorelasi dengan Jenis Kelamin yang menjadi variabel interest. Sehingga nilai VIF Jenis Kelamin rendah.

Nilai VIF tinggi yang disebabkan oleh sebab inklusi karena hasil perkalian atau kuadrat di dalam model, namun kedua variabel tersebut berkorelasi kuat terhadap hasil perkaliannya.

Misalkan model kita terdapat variabel bebas X1, X2 dan X1*X2. Dimana X1*X2 adalah hasil perkalian X1 dan X2. Kita ilustrasikan dengan cara melakukan Standarisasi berdasarkan data yang digunakan pada contoh di atas (Dataset Multikolinearitas). Standarisasi kita lakukan pada semua variabel, baik X1, X2 dan Y sebelum kita kalikan antara X1 dan X2. Setelah distandarisasi baik X1 dan X2, selanjutnya variabel baru hasil standarisasi tersebut kita kalikan, misal kita beri nama hasil standarisasi X1 menjadi SX1, X2 menjadi SX2 dan Y menjadi SY. Kita kalikan SX1 dengan SX2 menjadi SX1X2. Selanjutnya kita lakukan uji regresi linear dengan model: SY = Alpha + Beta1 SX1 + Beta2 SX2 + Beta3 SX1X2 + e.

Dengan sumber data yang sama, kita lihat hasilnya di bawah ini:

Perhatikan di atas: Nilai Standar error rendah, rentang lower dan upper bound sempit, serta Signifikansi t parsial tetap signifikan. Kalau kita telusuri nilai VIFnya, perhatikan di bawah ini:

Lihat bahwa nilai VIF tetap rendah, yaitu < 5 atau < 10.

Model regresi dengan variabel dummy dengan jumlah kategori variabel dummy adalah tiga kategori atau lebih.

Dikatakan tidak akan menjadi masalah jika terdapat perbedaan jumlah yang mencolok anggota sampel didalam kategori, dimana yang menjadi kategori referensi adalah kategori yang jumlah anggotanya sedikit. Sebagai contoh: jumlah sampel sebanyak 100 orang. Variabel Dummy adalah “Jenis Pekerjaan (Petani, Buruh, PNS)”. Anggota kategori Petani 45 orang, Buruh 45 orang, sedangkan PNS 10 orang. Selanjutnya yang menjadi referensi adalah yang anggotanya sedikit, yaitu PNS. Hal ini menyebabkan Variabel Dummy tidak akan berkorelasi terhadap variabel lainnya, sebab yang menjadi referensi adalah yang jumlah anggotanya paling sedikit.

Cara Mengatasi Multikolinearitas

Cara mengatasi multikolinearitas adalah dengan cara:

1. Jika jumlah variabel banyak, maka kita dapat melakukan Analisis Faktor sebelum regresi. Setelah analisis faktor, variabel baru yang terbentuk kita gunakan sebagai variabel di dalam model regresi.
2. Dengan cara memilih salah satu diantara variabel bebas yang berkorelasi kuat. Oleh karena itu, sebelumnya anda harus mencari variabel yang nilai VIFnya tinggi dan nilai korelasinya dengan variabel bebas lainnya kuat.
3. Dengan cara melakukan operasi matematis antar variabel bebas yang berkorelasi kuat sehingga didapat variabel baru hasil operasi tersebut yang kemudian dimasukkan ke dalam model regresi sebagai perwakilan dari variabel yang menjadi sumber operasi matematis tersebut.
4. Melakukan standarisasi terhadap variabel yang menjadi penyebab inklusi perkalian antara variabel, dimana hasil perkalian setelah standarisasi tersebut yang dimasukkan ke dalam model bersama-sama dengan variabel yang sudah distandarisasi.

Selanjutnya sampailah kita pada bahasan untuk melakukan uji multikolinearitas menggunakan aplikasi SPSS. Bagaimana cara uji multikolinearitas dengan SPSS? Akan kita bahas pada artikel selanjutnya yaitu Uji Multikolinearitas.

By Anwar Hidayat