Rumus Somer’s D
Pengertian Rumus Somer’s D
Uji Somer’s D adalah salah satu dari uji Asosiatif Non Parametris. Somer’s D mengukur hubungan antara 2 variabel berskala ordinal yang dapat dibentuk ke dalam tabel kontingensi. Uji ini mengukur hubungan yang bersifat symmetris artinya variabel A dan variabel B dapat saling mempengaruhi. Rumus Somer’s diciptakan oleh Robert H. Somers. Rumus Somer’s D ini merupakan penyempurnaan dari rumus Gamma dengan memperhatikan TIES dan merupakan modifikasi dari rumus Kendall Tau -b.

Kelebihan Somer’s D
Kelebihan dari rumus ini dapat menentukan arah hubungan, apakah variabel Y sebagai variabel dependen, X sebagai Variabel dependen atau hubungan keduanya simetris. Sehingga apabila anda menilai hubungan 2 variabel ordinal dengan bentuk tabel kontingensi dan ada variabel yang mempengaruhi serta ada variabel yang dipengaruhi, maka rumus Somer’s D sangatlah tepat digunakan.
Berikut rumus Somer’s D x-y (Variabel Y Sebagai Dependen):

Keterangan:
Ns: Concordant (P)
Nd: Discordant (Q)
Ty: Pasangan Kolom
Somer’s D x-y = Concordant-Discordant/Concordant+Discordant+Pasangan Kolom
Apabila Variabel X Sebagai Dependen atau hubungan simetris, rumus sebagai berikut:
Somer’s D y-x = Concordant-Discordant/Concordant+Discordant+Pasangan Baris
ganti Ty dengan Tx
Somer’s D sym = Concordant-Discordant/Concordant+Discordant+(Pasangan Kolom+Pasangan Baris/2)
Ganti Ty dengan (Tx+Ty)/2
Contoh Uji Somer’s D
Contoh: Peringkat Pengetahuan baik, respondennya ada 23 sampel dan peringkat pengetahuan kurang ada 12 sampel. Itulah yang disebut TIES.
Lihat Diagram di bawah ini:
Keterangan:
Pasangan Q adalah pasangan discordant karena X1 lebih rendah dari X2 tetapi Y3 lebih tinggi dari Y2, atau bisa juga dinyatakan X2 lebih tinggi dari X1 tetapi Y2 lebih rendah dari Y3. Pasangan P adalah pasangan concordant karena X2 lebih rendah X3 dan Y2 lebih rendah dari Y3, atau bisa juga dinyatakan X3 lebih tinggi dari X2 dan Y3 lebih tinggi dari Y2. Jadi bisa dikatakan pasangan concordant menunjukkan perubahan ranking pada variabel X searah dengan perubahan ranking pada Variabel Y, sedangkan pasangan discordant menunjukkan perubahan ranking pada variabel X tidak searah dengan perubahan ranking pada Variabel Y. Banyaknya pasangan searah (concordant) dan tidak serarah (discordant) itulah yang menjadi dasar perhitungan statistik Gamma.
Pasangan Tx dan Ty tidak akan digunakan pada uji Gamma (Pada Tau -b dan Somer’s D).
Berikut Contoh perhitungan Uji Somer’s D:
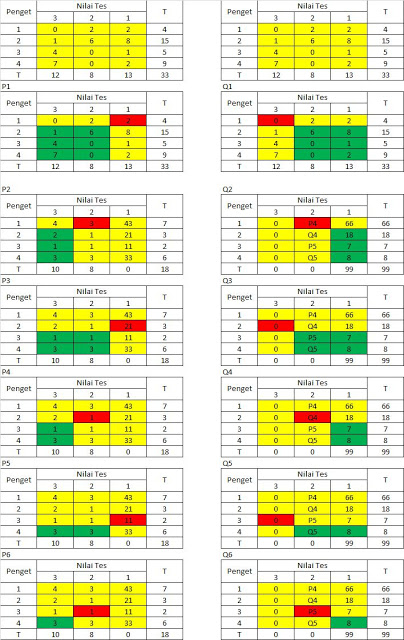
Cara hitung P dan Q:
Pada Gambar tabel-tabel di atas, lihat warna merah dan hijau. Cara menghitung P adalah mengkalikan Cell dimulai dari kanan atas (warna merah) dengan jumlah cell-cell di kiri bawahnya (warna hijau). Cara menghitung Q adalah mengkalikan Cell di mulai dari kiri atas (warna merah) dengan jumlah cell-cell di kanan bawahnya (warna hijau):
Contoh di atas pada jumlah sampel N=33.
P1: 2(6+1+0+4+0+7)=36.
P2: 2(1+4+7)=24
P3: 8(0+4+0+7)=88
P4: 6(4+7)=66
P5: 1(0+7)=7
P6: 0(7)=0
Jadi nilai total P=36+24+88+66+7+0=221
Q1: 0(6+8+0+1+0+2)=0
Q2: 2(8+1+2)=22
Q3: 1(0+1+0+2)=3
Q4: 6(1+2)=18
Q5: 4(0+2)=8
Q6: 0(2)=0
Jadi nilai total Q=51
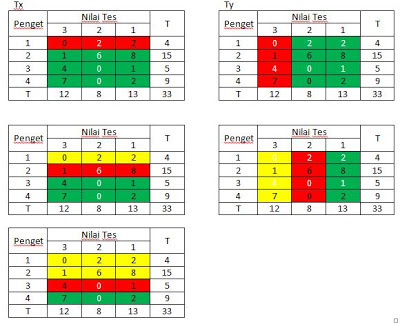
Cara Hitung Tx dan Ty:
Pada Gambar tabel-tabel di atas, lihat warna merah dan hijau. Cara menghitung Tx adalah mengkalikan Cell dimulai dari paling atas (warna merah) dengan jumlah cell-cell di bawahnya (warna hijau). Cara menghitung Ty adalah mengkalikan Cell di mulai dari paling kiri (warna merah) dengan jumlah cell-cell di kanannya (warna hijau):
Tx1: 0(1+4+7)=0
Tx2: 2(6+0+0)=12
Tx3: 2(8+1+2)=22
Tx4: 1(4+7)=28
Tx5: 8(1+2)=16
Tx6: 6(0+0)=0
Tx7: 4(7)=28
Tx8: 0(0)=0
Tx9: 1(2)=2
Jadi nilai total Tx=0+12+22+28+16+0+28+0+2=99
Ty1: 0(2+2)=0.
Ty2: 1(6+8)=48
Ty3: 4(0+1)=4
Ty4: 7(0+2)=14
Ty5: 2(2)=4
Ty6: 6(8)=48
Ty7: 0(1)=0
Ty8: 0(2)=0
Jadi nilai total Q=84
Hasil Perhitungan Somer’s D
Somer’s D x-y = P-Q/P+Q = (221-51)/(221+51+84) = 0,478.
Somer’s D y-x = P-Q/P+Q = (221-51)/(221+51+99) = 0,458.
Somer’s D sym = P-Q/P+Q = (221-51)/(221+51+((99+84)/2)) = 0,468.
Nilai Somer’s disebut sebagai koefisien korelasi Somer’s D, di mana D berkisar antara -1 (hubungan tidak searah sempurna) dan +1 (hubungan searah sempurna).
Hasil uji di atas:
Variabel Y Sebagai Dependen: D = 0,478 berarti hubungan kedua variabel sedang.
Variabel X Sebagai Dependen: D = 0,458 berarti hubungan kedua variabel sedang.
Hubungan Simetris: 0,468 berarti hubungan kedua variabel sedang.
Tetapi apakah secara statistik, nilai koefisien korelasi tersebut bermakna atau tidak? maka diperlukan uji selanjutnya, yaitu uji signifikansi. Bagaimana caranya? Pada Uji Somer’s D, dengan mendapatkan nilai z score yang akan dibandingkan dengan z tabel.
Z score pada uji Somer’s:
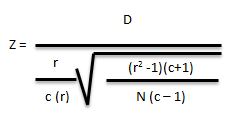
Keterangan:
D: Koefisien Somer’s D
r: Jumlah baris
c: Jumlah kolom
N: Sampel
Perhitungan pada contoh Z Score Somer’s D x-y:

Zx-y = 3,35971
Zy-x = 3,22387
Zsym = 3,29039
Cara pengambilan keputusan:
Apabila -Z Score < -Z Tabel atau +Z Score > +Z Tabel, maka ada hubungan yang siginifikan atau H1 diterima dan H0 Ditolak.
Contoh di atas menunjukkan Z Score 2,29861 pada derajat kepercayaan 95% atau batas kritis 0,05 pada uji 2 sisi (0,025) > Z Tabel +1,96 atau -2,29861 < -1,96, maka berarti ada hubungan yang siginifikan atau H1 diterima dan H0 Ditolak.
Untuk lebih jelasnya, baca artikel tentang z tabel dan interprestasinya:
By Anwar Hidayat

















Mantap bro..
Terima Kasih
kak bikin tutorial uji somer’s d pake spss atau minitab song
Ya