Tutorial Cara Uji Normalitas dengan STATA

Uji Normalitas dengan STATA

Uji Normalitas dengan STATA yang dapat dilakukan antara lain: uji Shapiro Wilk, Shapiro Francia, Skewness Kurtosis dan metode grafik. Kita telah mempelajari berbagai jenis uji normalitas pada artikel-artikel sebelumnya, antara lain:

1. Normalitas Pada SPSS
2. Normalitas Pada Minitab
3. Uji Normalitas (Chi-Square Goodness of Fit Test Normalitas)
4. Rumus Kolmogorov
5. Rumus Shapiro Wilk
6. Rumus Lilliefors
7. Kolmogorov Smirnov dalam SPSS
8. Kolmogorov dalam Excel
9. Lilliefors dalam Excel

Dalam artikel kali ini, kita akan membahas 3 uji normalitas yang banyak memiliki kelebihan dibandingkan dengan uji normalitas lainnya. 3 Uji tersebut dapat kita gunakan dalam Aplikasi STATA. Dalam artikel ini juga dibahas bagaimana cara mendeteksi normalitas dengan metode grafik dalam STATA.

Tiga Uji tersebut antara lain: Shapiro Wilk, Shapiro Francia dan Skewness Kurtosis.

Shapiro Wilk

Shapiro-Wilk test merupakan uji yang paling direkomendasikan oleh banyak ahli karena paling bagus dalam mendeteksi normalitas. Kami telah membahas mengenai uji ini pada artikel-artikel sebelumnya dan cara aplikasinya dalam SPSS maupun menggunakan rumus manual. Uji ini dikemukakan oleh Shapiro dan Wilk pada tahun 1965.

Kelebihan dari uji ini adalah sangat efektif digunakan pada sampel sebanyak 7 s/d 50 responden, di mana uji yang lain tidak reliable pada jumlah sampel yang kecil.

Kelemahan dari uji ini adalah hanya efektif digunakan pada sampel kurang dari 2000. Apabila lebih dari 2000 sudah tidak reliable lagi.

Shapiro Francia

Shapiro-Francia test dikemukakan oleh Shapiro dan Francia pada tahun 1972 untuk memperbaiki uji Shapiro-Wilk. Royston (1982) menyatakan bahwa uji ini valid pada jumlah sampel 3 s/d 2000. Namun pada Stata tetap dapat dilakukan pada sampel 5 s/d 5000.

Shapiro-Francia test adalah uji normalitas yang merupakan pengembangan dari Shapiro-Wilk Test. Hasil yang ditunjukkan selalu hampir sama dengan hasil Shapiro-Wilk. Meski pada sampel kecil tidak sehandal Shapiro-Wilk, namun banyak ahli yang merekomendasikan uji ini. Kelebihannya adalah tetap reliabel hingga jumlah sampel sebanyak 5000, di mana Shapiro-Wilk sudah tidak reliable lagi. Namun apabila lebih dari 5000 maka uji ini sudah tidak reliable.

Skewness-Kurtosis Test

Skewness-Kurtosis Test diperkenalkan Oleh D’Agostino dan Belanger pada tahun 1990. Bisa dikatakan uji ini merupakan uji yang paling reliable diantara yang lain, sebab akan tetap mendeteksi ketidak-normalan pada jumlah sampel berapapun, baik jumlah kecil maupun besar.

Pada Stata ada 2 pilihan uji ini, yaitu dengan Royston Adjusment dan tanpa Royston Adjusment.

Tutorial Uji Normalitas dengan STATA

Untuk mempermudah tutorial, silahkan anda download file kerja STATA tutorial ini: Normalitas.dta.

• Isi Data dengan cara: Pada Menu Klik Data, Data Editor, Data Editor (Edit), Kemudian isi.
• Langkah Pertama adalah melakukan Uji Shapiro-Wilk, dengan cara pada Menu, klik Statistics, kemudian klik (Summaries, tables and tests), Distributional plots and test, Pilih Shapiro-Wilk Normality Test. Pada Combobox variable, pilih variabel yang akan diuji.
• Langkah Kedua adalah melakukan Uji Shapiro-Francia, dengan cara pada Menu, klik Statistics, kemudian klik (Summaries, tables and tests), Distributional plots and test, Pilih Shapiro-Francia Normality Test. Pada Combobox variable, pilih variabel yang akan diuji.
• Langkah Ketiga adalah melakukan Uji Shapiro Wilk, dengan cara pada Menu, klik Statistics, kemudian klik (Summaries, tables and tests), Distributional plots and test, Pilih Skewness and Kurtosis Normality Test. Jangan Centang Suppress Royston Adjusment. Pada Combobox variable, pilih variabel yang akan diuji.
• Langkah Keempat adalah melakukan Uji Shapiro Wilk, dengan cara pada Menu, klik Statistics, kemudian klik (Summaries, tables and tests), Distributional plots and test, Pilih Skewness and Kurtosis Normality Test. Centang Suppress Royston Adjusment. Pada Combobox variable, pilih variabel yang akan diuji.
• Lihat Output

Interprestasi Output Uji Normalitas STATA

Shapiro Wilk

. swilk var1

Shapiro-Wilk W test for normal data

Variable |    Obs       W             V             z        Prob>z
————-+————————————————–
var1 |    100    0.99464      0.442    -1.810    0.96485

Lihat nilai Prob>z. Pada contoh di atas nilainya 0,96485 lebih dari 0,05, maka data berdistribusi Normal.

Shapiro Francia

. sfrancia var1

Shapiro-Francia W’ test for normal data

Variable |    Obs       W’            V’           z          Prob>z
————-+————————————————–
var1 |    100    0.99764      0.214    -3.300    0.99952

Lihat nilai Prob>z. Pada contoh di atas nilainya 0,99952 lebih dari 0,05, maka data berdistribusi Normal.

Skewness Kurtosis

. sktest var1

Skewness/Kurtosis tests for Normality
——- joint ——
Variable |    Obs   Pr(Skewness)   Pr(Kurtosis)  adj chi2(2)    Prob>chi2
————-+—————————————————————
var1 |       100      0.8613              0.2856          1.20            0.5498

Lihat nilai Prob>chi2. Pada contoh di atas nilainya 0,5498 lebih dari 0,05, maka data berdistribusi Normal.

Skewness Kurtosis (Suppress Royston Adjusment)

. sktest var1, noadjust

Skewness/Kurtosis tests for Normality
——- joint ——
Variable |    Obs   Pr(Skewness)   Pr(Kurtosis)      chi2(2)    Prob>chi2
————-+—————————————————————
var1 |      100      0.8613              0.2856            1.17        0.5569

Lihat nilai Prob>chi2. Pada contoh di atas nilainya 0,5569 lebih dari 0,05, maka data berdistribusi Normal.

Untuk memperkuat kesimpulan di atas, pada aplikasi STATA kita bisa menggunakan beberapa diagram. Namun bedanya dengan SPSS, kita tidak bisa otomatis mendapatkan berbagai diagram. Berikut langkahnya:

Histogram

Pada Menu, Klik Graphics, Distributional Graphs, Histogram, Kemudian isi Combobox Variabel dengan Variabel yang akan diuji. Klik OK.

Contoh di atas, membentuk kurve normal, maka variabel berdistribusi normal.

Normal QQ Plots

Pada Menu, Klik Graphics, Distributional Graphs, Normal quantile plot, Kemudian isi Combobox Variabel dengan Variabel yang akan diuji. Klik OK.

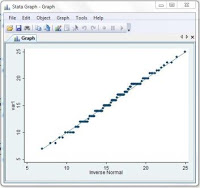
Contoh di atas, plot-plot mengikuti garis fit line, maka variabel berdistribusi normal.

Normal PP Plots

Pada Menu, Klik Graphics, Distributional Graphs, Normal probability plot, Kemudian isi Combobox Variabel dengan Variabel yang akan diuji. Klik OK.

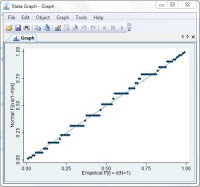
Contoh di atas, plot-plot mengikuti garis fit line, maka variabel berdistribusi normal.

Stem-Leaf

Pada Menu, klik Statistics, kemudian klik (Summaries, tables and tests), Distributional plots and test, Pilih Steam-and-leaf display., Kemudian isi Combobox Variabel dengan Variabel yang akan diuji. Klik OK.

Contoh di atas, angka-angka membentuk kurve normal miring ke arah kanan, maka variabel berdistribusi normal.

Box-Plot

Pada Menu, Klik Graphics, Distributional Graphs, Box Plot, Kemudian isi Combobox Variabel dengan Variabel yang akan diuji. Klik OK.

Contoh di atas, box berada ditengah dengan kedua kaki yang sama panjang, garis horizontal berada ditengah box dan tidak terdapat plot-plot di atas atau di bawah box, maka variabel berdistribusi normal.

Untuk contoh diagram yang menunjukkan distribusi tidak normal, lihat di bawah ini:

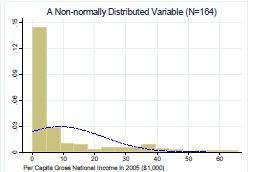
SEMOGA BERMANFAAT

Artikel Berikutnya: Memilih Transformasi Data dengan STATA

By Anwar Hidayat